io7m | single-page | multi-page | epub | Calino 1.0

Calino 1.0

CREATOR Mark Raynsford
DATE 2022-01-15T17:18:45+00:00
DESCRIPTION Specification for the Calino texture file format.
IDENTIFIER ba8fa621-69a4-486d-b5d7-1c31f76eba32
LANGUAGE en
RIGHTS Public Domain
TITLE Calino 1.0

Table Of Contents

1. Overview

1
This specification defines version 1.0 of the calino file format. The calino format is a carefully designed file format intended for the storage and delivery of texture data for realtime 3D rendering applications.
2
This specification is divided into an abstract model and a separate binary encoding. The purpose of the model is to describe the semantics of calino files; the actual meaning of the data within, and to describe properties and invariants that must be true for all valid calino files. The purpose of the binary encoding is to describe how the model is transformed to a sequence of bytes/octets; it describes the low-level on-disk format of calino files. This layered approach is intended to allow for specifying the format with a level of precision that will allow data in the calino format to remain readable for decades into the future, and in a manner that ensures that the format is not dependent on any present-day rendering APIs.
3
Developers wishing to write their own code to read and write calino files might find it easiest to view the binary encoding section first. The calino format is designed to be straightforward to parse, requiring only a few minimal primitives to express the entirety of the format, and requires no references to external specifications (unlike many other image/texture file formats) [1]. Once a developer is able to read data from an existing calino file, they should consult the model to understand what the data they're receiving actually means. The model chapters are arranged in dependency order starting with the most fundamental concepts, and ending with the top level definitions of the various texture types.

Footnotes

1
It would be more accurate to say that the calino specification does not depend on any other specifications that are at the same level of abstraction. For example, the calino specification makes references to Unicode, IEEE-754, and so on. It does not, however, require understanding any other existing texture formats, or depend on any definitions given in the specifications for any rendering APIs.
References to this footnote: 1

2. Notational Conventions

2.1. Gallina/Coq

1
The formal specification described here is written in the Gallina specification language of the Coq theorem prover. The language is a total, pure-functional, dependently-typed language allowing for describing systems in rigorous detail including machine-checked proofs of various chosen properties.
2
Readers are not expected to be able to understand the bodies of the proof texts, and doing so is not in any case required. As long as one can understand the meaning of the propositions being expressed, it suffices to trust that the proofs are correct as they are all machine-checked whenever the specification is published.
3
The full sources of the entire specification are published at the end of this book.

2.2. Unicode

1
The specification makes reference to the Unicode character set which, at the time of writing, is at version 13.0.0. The specification often references specific Unicode characters, and does so using the standard notation U+NNNN, where N represents a hexadecimal digit. For example, U+03BB corresponds to the lowercase lambda symbol λ.

2.3. Sets

1
Where the specification refers to sets, it is referring to sets as defined in Zermelo-Fraenkel set theory.

2.3.2. ZFC

Notation Description
e ∈ A e is an element of the set A
e ∉ A e is not an element of the set A
{ x₀, x₁, ... xₙ } A set consisting of values from x₀ to xₙ
{ e ∈ A | p(e) } A set consisting of the elements of A for which the proposition p holds
|A| The cardinality of the set A; a measure of the number of elements in A
∅ The empty set
𝔹 The booleans
ℕ The natural numbers
ℝ The real numbers
ℤ The integers
[a, b] A closed interval in a set (given separately or implicit from the types of a and b), from a to b, including a and b
(a, b] A closed interval in a set (given separately or implicit from the types of a and b), from a to b, excluding a but including b
[a, b) A closed interval in a set (given separately or implicit from the types of a and b), from a to b, including a but excluding b
(a, b) A closed interval in a set (given separately or implicit from the types of a and b), from a to b, excluding a and b
A ⊂ B A is a subset of, and is not equal to, B
A ⊆ B A is a subset of, or is equal to, B
A ∩ B The smallest set of elements that appear in both A and B (intersection).

3. The Calino Model

3.1. Overview

1
The calino texture file format is optimized for the storage of textures used for real-time 3D rendering. The format provides the following features:

3.1.2. Features

  • Detailed information about the format and layout of image data is included in all files. Image data, in the common case, can be introspected without requiring consulting any kind of external specification. The information provided about image data includes dimensions, full channel layout and type information, compression and supercompression methods, color space, coordinate system, alpha premultiplication, and byte ordering for formats that use components larger than a single octet.
  • Mipmaps are natively supported and are not treated differently to textures that do not have mipmaps; an texture without mipmaps is considered to comprise of a single mip level 0. Mipmaps are exposed in a manner that facilitates efficient texture streaming.
  • Rendering system independence. The format specification does not require implementers to read the Vulkan, OpenGL, DirectX specifications in order to parse files.
  • Ease of parsing. The binary format is designed to facilitate easy and secure parsing without requiring backtracking or unbounded storage use. A competent developer should be able to implement a full parser within a week or two of work.
  • Carefully layered metadata. Consumers are not required to understand everything about the underlying image data in order to make use of it. For example, if image data is encoded using an unusual and/or proprietary texture format (such as A5B3G3R3), consumers can still trivially extract the raw data of each mipmap even if they cannot necessarily perform rendering with image data of that format. Likewise, the compressed bytes of each mipmap can always be obtained even if the compression method is unknown to the consumer.
  • Extensibility. The format consists of explicitly-sized sections with a well-defined ordering. Consumers can trivially skip sections that they do not understand. Sections carry unique 64-bit identifiers; if a section has an identifier not recognized by a consumer, the consumer may skip the section. The raw bytes that comprise a section can be extracted regardless of whether or not the consumer understands them. This specification defines a number of "standard" image data types that consumers are expected to understand, but the format also allows for declaring new self-describing image data types.
  • Practical metadata. The format provides a standard section that contains UTF-8 encoded keys and values intended to hold arbitrary metadata. Metadata that cannot be expressed as a UTF-8 string can be included as a custom section that can be skipped by consumers that do not recognize it.
3
This section of the specification documents the abstract model that the calino format uses to express all of the above.

3.2. Divisibility By 8

1
This specification makes frequent use of values that must be evenly divisible by 8. Formally, a number n is evenly divisible by 8 if n mod 8 = 0.

3.2.2. Divisible8

Definition divisible8 (x : nat) : Prop :=
  modulo x 8 = 0.
3
The property of being divisible by 8 is preserved over addition. That is, if two numbers n and m are divisible by 8, then n + m is divisible by 8.

3.2.4. Divisible8 Addition

Theorem divisiblity8Add : ∀ (x y : nat),
  divisible8 x → divisible8 y → divisible8 (x + y).
Proof.
  (* Proof omitted for brevity; see Divisible8.v for proofs. *)
Qed.

3.3. Bits & Octets

1
A bit is a single digit in the base-2 numbering system. A bit may either be 0 or 1:

3.3.2. Bit

Inductive bit : Set :=
  | B0
  | B1.
3
A sequence of bits may be divided into groups of eight bits known as octets. We avoid the use of the term byte because a byte hasn't consistently been equivalent to eight bits throughout all of computing history. An octet may either be exact or a remainder. An octet may be a remainder if the length of the sequence of bits used to produce it was not evenly divisible by 8. The first n groups of 8 bits consumed from a sequence of bits s will produce octets that are exact, with the remaining k bits (where k < 8) will produce at most one remainder octet. The remainder octet, if any, has it's least significant 8 - k bits set to 0.

3.3.4. Octet

Inductive octet : Set :=
  | OctExact  : bit → bit → bit → bit → bit → bit → bit → bit → octet
  | OctRemain : bit → bit → bit → bit → bit → bit → bit → bit → octet.
5
The sequence of bits s will be consumed in order such that octets are filled from most significant to least significant bit order.
6
If the sequence of octets o produced is arranged such that the first bit of s appears as the most significant bit of the first octet in o, then o is said to be in big-endian order.

3.3.7. Big Endian Octets (Aux)

Fixpoint octetsBigEndianAux
  (bits   : list bit)
  (octets : list octet)
: list octet :=
  match bits with
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: rest) =>
    octets ++ [OctExact b7 b6 b5 b4 b3 b2 b1 b0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 b2 b1 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 b2 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: rest) =>
    octets ++ [OctRemain b7 b6 B0 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: rest) =>
    octets ++ [OctRemain b7 B0 B0 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | [] =>
    octets
  end.

3.3.8. Big Endian Octets

Definition octetsBigEndian (bits : list bit) : list octet :=
  octetsBigEndianAux bits [].
9
If the sequence of octets o produced is arranged such that the first bit of s appears as the most significant bit of the last octet in o, then o is said to be in little-endian order.

3.3.10. Little Endian Octets

Definition octetsLittleEndian (bits : list bit) : list octet :=
  rev (octetsBigEndianAux bits []).
11
A sequence of bits s such that divisible8 (length s) will produce a sequence consisting of entirely exact octets.

3.3.12. Divisible8 Exact Octets (Big endian)

Theorem octetsBigEndianLengthDivisibleAllExact : ∀ (b : list bit),
  divisible8 (length b) → Forall octetIsExact (octetsBigEndian b).
Proof.
  (* Proof omitted for brevity; see ByteOrder.v for proofs. *)
Qed.

3.3.13. Divisible8 Exact Octets (Little endian)

Theorem octetsLittleEndianLengthDivisibleAllExact : ∀ (b : list bit),
  divisible8 (length b) → Forall octetIsExact (octetsLittleEndian b).
Proof.
  (* Proof omitted for brevity; see ByteOrder.v for proofs. *)
Qed.
14
A sequence of bits s such that ¬ divisible8 (length s) will produce a remainder octet.

3.3.15. Divisible8 Exact Octets (Big endian)

Theorem octetsBigEndianLengthIndivisibleRemainder : ∀ (b : list bit),
  0 < length b mod 8 → ∃ o, In o (octetsBigEndian b) ∧ octetIsRemainder o.
Proof.
  (* Proof omitted for brevity; see ByteOrder.v for proofs. *)
Qed.

3.3.16. Divisible8 Exact Octets (Little endian)

Theorem octetsLittleEndianLengthIndivisibleRemainder : ∀ (b : list bit),
  0 < length b mod 8 → ∃ o, In o (octetsLittleEndian b) ∧ octetIsRemainder o.
Proof.
  (* Proof omitted for brevity; see ByteOrder.v for proofs. *)
Qed.

3.4. Descriptors

1
A descriptor is a UTF-8 encoded string of an arbitrary length that describes an object in a calino texture file.

3.4.2. Descriptor

Definition descriptor := string.
3
An object is describable iff it has an associated descriptor.

3.4.4. Describable

Class describable (A : Set) := {
  descriptorOf : A -> descriptor
}.
5
This specification defines the descriptors that must be returned for various objects in the specification by giving function definitions that map values to descriptor strings.

3.5. Channels

3.5.1. Overview

1
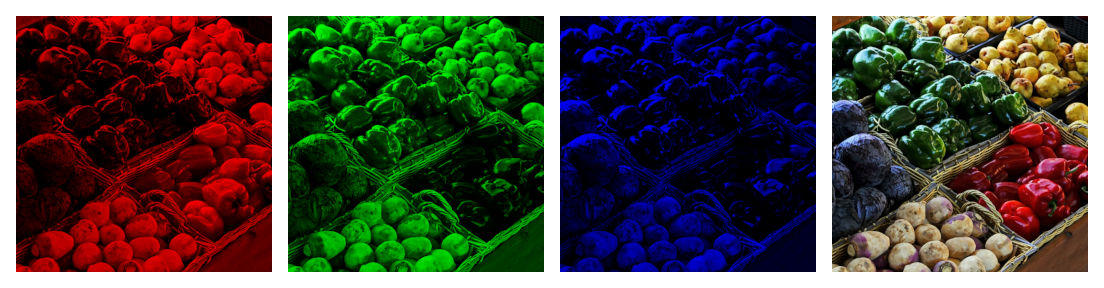
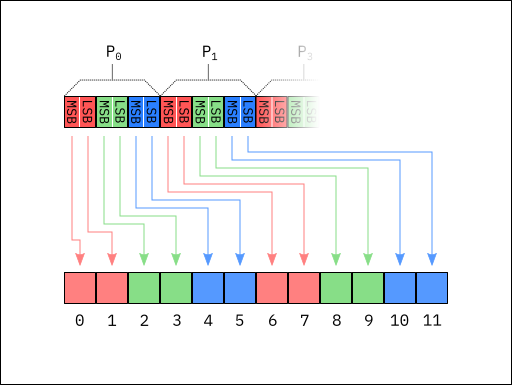
A channel in calino corresponds to the traditional definition of a channel in computer graphics: A channel consists of a set of intensity values for one of the color components that make up an image. For example, a typical RGB image has a red channel, a green channel, and a blue channel that store the intensity values of each component for each pixel in the image. The following image shows the separate red, green, and blue channels used for the pixels of an RGB image:

3.5.1.2. RGB Example

A picture of some produce divided into separate color channels.
3
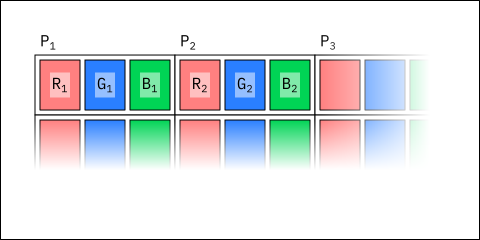
As the calino package is intended for use in real-time 3D graphics, it makes the assumption that for an image consisting of channels [c₁, cₙ], each pixel Pᵢ in the image stores channel values [c₁(ᵢ), cₙ (ᵢ)] sequentially in memory:

3.5.1.4. Channels Example

Channel data laid out sequentially in memory.
5
A set of channels may be packed or unpacked. In an unpacked set of channels, each channel is of a size in bits that is a multiple of 8. This means that when the set of channels is stored in memory for each pixel, each channel occupies at least one octet in memory, and no two channels in a given pixel occupy the same octet. For channels that are larger than a single octet, the byte ordering of the underlying host computer dictates the exact order of the octets that make up a single channel. 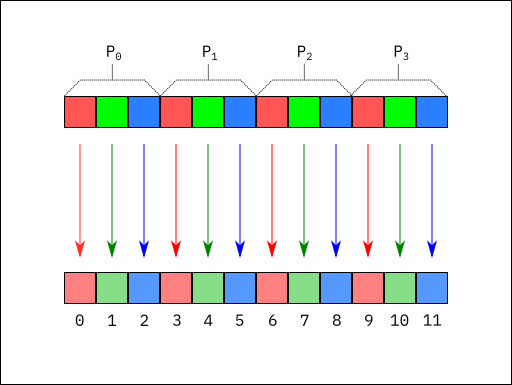Otherwise, the groups of octets that comprise the data for a set of channels are ordered according to the channel declaration order. For example, a common unpacked image format in computer graphics, at the time of writing, is R8G8B8. In the R8G8B8 format, each channel occupies 8 bits, and the channels are stored such that R comes first in memory, followed by G, and then B:

3.5.1.6. R8G8B8

Image showing R8G8B8 stored in memory.
7
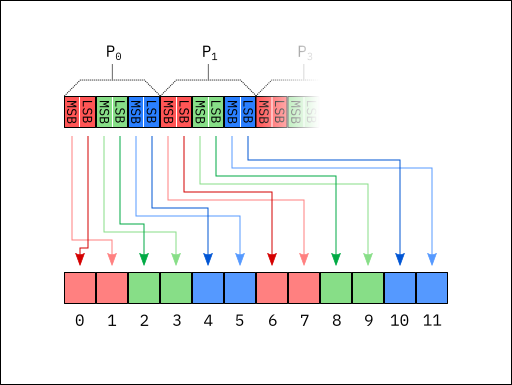
Note that, because all of the channels are 8 bits, the mapping from the channels to the underlying host octets does not depend on the byte ordering of the underlying host computer. Another common unpacked image format where the underlying byte ordering of the host computer does affect the mapping from channels to octets is the R16G16B16 format. In the R16G16B16 format, each channel requires 16 bits and so each channel must be mapped to two octets in memory. If the underlying host byte ordering is little-endian, then the most significant bits of each channel are stored in the lower of the two octets used for the channel. If the underlying host byte ordering is big-endian, then the most significant bits of each channel are stored in the higher of the two octets used for the channel. For example, channels in the R16G16B16 format are stored as follows on a computer with little-endian byte ordering:

3.5.1.8. R16G16B16 Little Endian

Image showing R16G16B16 stored in little-endian memory.
9
As shown in the diagram, the 8 most significant bits of the R channel of pixel 0 are stored in octet 1. The 8 least significant bits of the R channel of pixel 0 are stored in octet 0. This pattern continues for each subsequent channel of each subsequent pixel. Note that regardless of the byte ordering, the octets that make up the R channel are stored first, followed by the G channel, and finally the B channel. The same format on a computer with big-endian byte ordering is stored as follows:

3.5.1.10. R16G16B16 Big Endian

Image showing R16G16B16 stored in big-endian memory.
11
As shown in the diagram, the 8 most significant bits of the R channel of pixel 0 are stored in octet 0. The 8 least significant bits of the R channel of pixel 0 are stored in octet 1. This pattern continues for each subsequent channel of each subsequent pixel. Note that regardless of the byte ordering, the octets that make up the R channel are stored first, followed by the G channel, and finally the B channel.
12
In a packed set of channels, each channel may be of any size in bits (excluding zero) but the sum of the sizes of all of the channels in the set typically must be a multiple of 8. The calino package restricts this definition further by stating that the sum of the sizes of the channels must be in the set {8, 16, 32, 64}. Conceptually, the bits of all channels are packed into a single integer value, and then this integer value is stored in memory according to the host computer byte ordering. 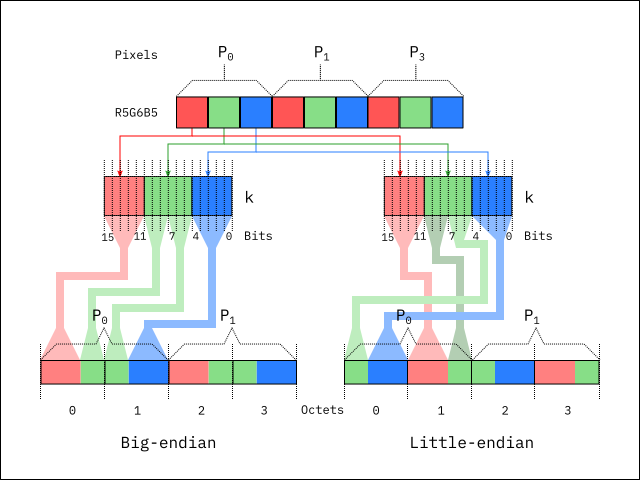For example, a common packed image format in computer graphics, at the time of writing, is R5G6B5. In the R5G6B5 format, the bits of all of the channels are packed into a single 16-bit integer k such that the 5 bits of the R channel are packed into the 5 most significant bits of k, followed by the 6 bits of the G channel, followed by the 5 bits of the B channel. The value of k is then stored into memory according to the host computer byte ordering:

3.5.1.13. R5G6B5

Image showing R5G6B5 stored in memory.
14
In the above diagram, it's clear that the 5 bits that make up the R channel of pixel 0 are mapped to bits [11,15] in k. The 6 bits that make up the G channel are mapped to bits [5, 14] in k, and the remaining 5 bits that make up the B channel are mapped to bits [0,4] in k. On a big-endian computer, the two octets that make up k are arranged such that the most significant bits of k end up in octet 0 in memory, whilst the least significant bits of k end up in octet 1 in memory. On a little-endian computer, the two octets that make up k are arranged such that the most significant bits of k end up in octet 1 in memory, whilst the least significant bits of k end up in octet 0 in memory. Note that this means that the G channel ends up divided into two pieces with the R and B channels sandwiched between it. It's also important to note that the ordering of bits does not change between big-endian and little-endian systems. This demonstrates the critical difference between packed and unpacked formats: In a packed format, any given octet may contain bits from more than one channel, whilst in an unpacked format, a given octet will contain bits from exactly one channel. At the time of writing, no rendering API appears to have defined any packed image formats that pack channels into an integer value larger than 32 bits.
15
The information provided about a set of channels largely attempts to answer two main questions: "How do I get image data to and from storage?" and "How do I interpret the image data once I have it?". Channel semantic and channel type information answers the latter question, whilst channel descriptions answer the former. The aggregates of these values, channel layouts, answer a little of both questions.

3.5.2. Channel Semantic

1
A channel semantic specifies how a particular channel should be interpreted within the context of an image. A channel semantic may be one of the following values:

3.5.2.2. Channel Semantic Values

Inductive channelSemantic : Set :=
  | CSRed
  | CSGreen
  | CSBlue
  | CSAlpha
  | CSDepth
  | CSStencil
  | CSExponent
  | CSUnused.
3
Channel semantic values must use the following descriptors:

3.5.2.4. Channel Semantic Description

Definition channelSemanticDescribe (c : channelSemantic) : descriptor :=
  match c with
  | CSRed      => "R"
  | CSGreen    => "G"
  | CSBlue     => "B"
  | CSAlpha    => "A"
  | CSDepth    => "D"
  | CSStencil  => "S"
  | CSExponent => "E"
  | CSUnused   => "X"
  end.

3.5.2.5. Channel Semantic Describable

Instance channelSemanticDescribable : describable channelSemantic := {
  descriptorOf c := channelSemanticDescribe c
}.

3.5.3. Channel Description

1
A channel description combines a channel semantic and a non-zero size value expressed in bits. The size value specifies the number of bits of storage required for a single value in the channel.

3.5.3.2. Channel Description

Inductive channelDescription : Set := channelDescriptionMake {
  cdSemantic    : channelSemantic;
  cdBits        : nat;
  cdBitsNonzero : 0 ≠ cdBits
}.
3
Channel descriptions must use the following descriptors:

3.5.3.4. Channel Description

Definition channelDescriptionDescribe (c : channelDescription) : descriptor :=
  descriptorOf (cdSemantic c) ++ stringOfNat (cdBits c).

3.5.3.5. Channel Describable

Instance channelDescriptionDescribable : describable channelDescription := {
  descriptorOf c := channelDescriptionDescribe c
}.
6
The descriptors for a set of channel descriptions must be concatenated together with U+003A ':':

3.5.3.7. Channel Descriptions

Fixpoint channelDescriptionsDescribe (c : list channelDescription) : descriptor :=
  match c with
  | nil        => ""
  | cons d nil => channelDescriptionDescribe d
  | cons d e   => (channelDescriptionDescribe d) ++ ":" ++ (channelDescriptionsDescribe e)
  end.

3.5.4. Channel Layout

3.5.4.1. Description

1
A channel layout describes how a set of channels are ordered. A channel layout may either be packed or unpacked.

3.5.4.1.2. Channel Layout

Inductive channelLayoutDescription : Set :=
  | ChannelLayoutDescriptionUnpacked : channelLayoutDescriptionUnpacked → channelLayoutDescription
  | ChannelLayoutDescriptionPacked   : channelLayoutDescriptionPacked   → channelLayoutDescription.
3
The total number of bits required by a set of channels is the sum of the sizes of each channel, as given by channelDescriptionsBitsTotal:

3.5.4.1.4. Channels Required Bits

Fixpoint channelDescriptionsBitsTotal (c : list channelDescription) : nat :=
  match c with
  | nil         => 0
  | (x :: rest) => (cdBits x) + (channelDescriptionsBitsTotal rest)
  end.
5
Both packed and unpacked layouts must always have a size in bits that is divisible by 8:

3.5.4.1.6. Channels Required Bits Divisible

Theorem channelLayoutDescriptionBitsDivisible8 : ∀ (c : channelLayoutDescription),
  divisible8 (channelLayoutDescriptionBits c).
Proof.
  (* Proof omitted for brevity; see ChannelDescription.v for proofs. *)
Qed.

3.5.4.2. Unpacked Layouts

1
An unpacked layout consists of a non-empty sequence of channels where the size of each channel must be divisible by 8.

3.5.4.2.2. Unpacked Layout

Inductive channelLayoutDescriptionUnpacked : Set := CLDUMake {
  uChannels         : list channelDescription;
  uChannelsNonEmpty : [] ≠ uChannels;
  uInvariants       : Forall channelDescriptionBitsDivisible8 uChannels;
}.

3.5.4.3. Packed Layouts

1
A packed layout consists of a non-empty sequence of channels and a layout packing value.

3.5.4.3.2. Packed Layout

Inductive channelLayoutDescriptionPacked : Set := CLDPMake {
  pChannels         : list channelDescription;
  pChannelsNonEmpty : [] ≠ pChannels;
  pPacking          : channelLayoutPacking;
  pInvariants       : channelDescriptionsBitsTotal pChannels = channelLayoutPackingBits pPacking
}.
3
The layout packing value must be one of the following values:

3.5.4.3.4. Layout Packing

Inductive channelLayoutPacking : Set :=
  | CLPack8
  | CLPack16
  | CLPack32
  | CLPack64.
5
The number of bits associated with a layout packing value is given by channelLayoutPackingBits:

3.5.4.3.6. Layout Packing Bits

Definition channelLayoutPackingBits (c : channelLayoutPacking) : nat :=
  match c with
  | CLPack8  => 8
  | CLPack16 => 16
  | CLPack32 => 32
  | CLPack64 => 64
  end.
7
The number of bits associated with a layout packing value is always divisible by 8:

3.5.4.3.8. Layout Packing Bits Divisible 8

Theorem channelLayoutPackingBitsDiv8 : ∀ c, divisible8 (channelLayoutPackingBits (c)).
Proof.
  (* Proof omitted for brevity; see ChannelDescription.v for proofs. *)
Qed.
9
For a packed layout, the number of bits required for the channels must equal the number of bits associated with the given packed layout.
10
Layout packing values are describable:

3.5.4.3.11. Layout Packing Description

Definition channelLayoutPackingDescribe (c : channelLayoutPacking) : descriptor :=
  match c with
  | CLPack8  => "p8"
  | CLPack16 => "p16"
  | CLPack32 => "p32"
  | CLPack64 => "p64"
  end.

3.5.4.3.12. Layout Packing Describable

Instance channelLayoutPackingDescribable : describable channelLayoutPacking := {
  descriptorOf c := channelLayoutPackingDescribe c
}.

3.5.4.4. Descriptors

1
Channel layouts are describable:

3.5.4.4.2. Unpacked Layout Description

Definition channelLayoutDescriptionUnpackedDescribe (c : channelLayoutDescriptionUnpacked) : descriptor :=
  channelDescriptionsDescribe (uChannels c).

3.5.4.4.3. Unpacked Layout Describable

Instance channelLayoutDescriptionUnpackedDescribable : describable channelLayoutDescriptionUnpacked := {
  descriptorOf c := channelLayoutDescriptionUnpackedDescribe c
}.

3.5.4.4.4. Packed Layout Description

Definition channelLayoutDescriptionPackedDescribe (c : channelLayoutDescriptionPacked) : descriptor :=
  let packing := descriptorOf (pPacking c) in
  let channels := channelDescriptionsDescribe (pChannels c) in
    packing ++ "|" ++ channels.

3.5.4.4.5. Packed Layout Describable

Instance channelLayoutDescriptionPackedDescribable : describable channelLayoutDescriptionPacked := {
  descriptorOf c := channelLayoutDescriptionPackedDescribe c
}.

3.5.4.4.6. Layout Description

Definition channelLayoutDescriptionDescribe (c : channelLayoutDescription) : descriptor :=
  match c with
  | ChannelLayoutDescriptionPacked p   => descriptorOf p
  | ChannelLayoutDescriptionUnpacked u => descriptorOf u
  end.

3.5.4.4.7. Layout Describable

Instance channelLayoutDescriptionDescribable : describable channelLayoutDescription := {
  descriptorOf c := channelLayoutDescriptionDescribe c
}.

3.5.5. Channel Type

1
A channel type defines how the sequence of bits that make up a value in a channel should be interpreted numerically. A channel type must be one of the following values:

3.5.5.2. Channel Types

Inductive channelType : Set :=
  | CTFixedPointNormalizedUnsigned
  | CTFixedPointNormalizedSigned
  | CTScaledUnsigned
  | CTScaledSigned
  | CTIntegerUnsigned
  | CTIntegerSigned
  | CTFloatIEEE754
  | CTCustom : descriptor → channelType.
3
A value of CTFixedPointNormalizedUnsigned indicates the values in a channel should be interpreted as unsigned fixed-point values. Given a floating point value f in the range [0, 1], the corresponding n-bit unsigned fixed point value h is given by the relation f = h / (2ⁿ - 1).
4
A value of CTFixedPointNormalizedSigned indicates that the values in a channel should be interpreted as signed fixed-point values. Given a floating point value f in the range [-1, 1], the corresponding n-bit signed fixed point value h is given by the relation f = max (h / (2ⁿ⁻¹ - 1), -1).
5
A value of CTScaledUnsigned indicates that the values in a channel should be interpreted as unsigned integers, and then converted to similar floating-point values on use. For example, a channel containing the value 23 would be ideally converted to 23.0 when sampled.
6
A value of CTScaledSigned indicates that the values in a channel should be interpreted as signed integers, and then converted to similar floating-point values on use. For example, a channel containing the value -23 would be ideally converted to -23.0 when sampled.
7
A value of CTIntegerUnsigned indicates that the values in a channel should be interpreted as unsigned integers.
8
A value of CTIntegerSigned indicates that the values in a channel should be interpreted as signed integers.
9
A value of CTFloatIEEE754 indicates that the values in a channel should be interpreted as IEEE 754 binary floating point values of a size appropriate for the channel (such as binary16, binary32, binary64, and etc).
10
A value of CTCustom indicates that values in a channel should be interpreted in a manner not defined by this specification. CTCustom values may be used, for example, to specify exotic platform-specific floating point formats for textures that are intended to be used on a limited range of hardware.
11
Channel types must use the following descriptors:

3.5.5.12. Channel Description

Definition channelTypeDescribe (c : channelType) : descriptor :=
  match c with
  | CTFixedPointNormalizedUnsigned => "FIXED_POINT_NORMALIZED_UNSIGNED"
  | CTFixedPointNormalizedSigned   => "FIXED_POINT_NORMALIZED_SIGNED"
  | CTScaledUnsigned               => "SCALED_UNSIGNED"
  | CTScaledSigned                 => "SCALED_SIGNED"
  | CTIntegerUnsigned              => "INTEGER_UNSIGNED"
  | CTIntegerSigned                => "INTEGER_SIGNED"
  | CTFloatIEEE754                 => "FLOATING_POINT_IEEE754"
  | CTCustom d                     => d
  end.

3.5.5.13. Channel Describable

Instance channelTypeDescribable : describable channelType := {
  descriptorOf c := channelTypeDescribe c
}.

3.5.6. Standard Formats

3.5.6.1. Overview

1
The calino package considers a number of formats to be standard at the time of writing due to their widespread use. In most cases, support for the formats is guaranteed to be present on modern GPUs due to their status of being required formats by specifications such as Vulkan.
2
Implementations must provide some degree of support for these formats. For example, implementations that provide tools to manipulate images must be able to, at a minimum, manipulate images in all of the standard formats. Packages that provide the ability to read calino texture files and upload the contents to a GPU must expect to encounter textures in all of the standard formats.

3.5.6.2. R4 G4 B4 A4

1
An RGBA layout with 4 bits of precision in each channel, packed into a 16-bit integer.

3.5.6.2.2. R4 G4 B4 A4 Definition

Definition Layout_R4_G4_B4_A4 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake R4_G4_B4_A4_Channels R4_G4_B4_A4_NonEmpty CLPack16 eq_refl).

3.5.6.3. A1 R5 G5 B5

1
An RGBA layout with 1 bit of precision in the alpha channel, and 5 bits of precision in each of the other channels, packed into a 16-bit integer.

3.5.6.3.2. A1 R5 G5 B5 Definition

Definition Layout_A1_R5_G5_B5 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake A1_R5_G5_B5_Channels A1_R5_G5_B5_NonEmpty CLPack16 eq_refl).

3.5.6.4. R5 G6 B5

1
An RGB layout with 5 bits of precision in the red and blue channels, and 6 bits of precision in the green channel, packed into a 16-bit integer.

3.5.6.4.2. R5 G6 B5 Definition

Definition Layout_R5_G6_B5 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake R5_G6_B5_Channels R5_G6_B5_NonEmpty CLPack16 eq_refl).

3.5.6.5. R8 G8 B8 A8

1
An unpacked RGBA layout with 8 bits of precision in each channel.

3.5.6.5.2. R8 G8 B8 A8 Definition

Definition Layout_R8_G8_B8_A8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_B8_A8_Channels R8_G8_B8_A8_NonEmpty R8_G8_B8_A8_FDiv8).

3.5.6.6. R8 G8 B8

1
An unpacked RGB layout with 8 bits of precision in each channel.

3.5.6.6.2. R8 G8 B8 Definition

Definition Layout_R8_G8_B8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_B8_Channels R8_G8_B8_NonEmpty R8_G8_B8_FDiv8).

3.5.6.7. R8 G8

1
An unpacked RG layout with 8 bits of precision in each channel.

3.5.6.7.2. R8 G8 Definition

Definition Layout_R8_G8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_Channels R8_G8_NonEmpty R8_G8_FDiv8).

3.5.6.8. R8

1
An unpacked R layout with 8 bits of precision in each channel.

3.5.6.8.2. R8 Definition

Definition Layout_R8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_Channels R8_NonEmpty R8_FDiv8).

3.5.6.9. R16 G16 B16 A16

1
An unpacked RGBA layout with 16 bits of precision in each channel.

3.5.6.9.2. R16 G16 B16 A16 Definition

Definition Layout_R16_G16_B16_A16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_B16_A16_Channels R16_G16_B16_A16_NonEmpty R16_G16_B16_A16_FDiv8).

3.5.6.10. R16 G16 B16

1
An unpacked RGB layout with 16 bits of precision in each channel.

3.5.6.10.2. R16 G16 B16 Definition

Definition Layout_R16_G16_B16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_B16_Channels R16_G16_B16_NonEmpty R16_G16_B16_FDiv8).

3.5.6.11. R16 G16

1
An unpacked RG layout with 16 bits of precision in each channel.

3.5.6.11.2. R16 G16 Definition

Definition Layout_R16_G16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_Channels R16_G16_NonEmpty R16_G16_FDiv8).

3.5.6.12. R16

1
An unpacked R layout with 16 bits of precision in each channel.

3.5.6.12.2. R16 Definition

Definition Layout_R16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_Channels R16_NonEmpty R16_FDiv8).

3.5.6.13. R32 G32 B32 A32

1
An unpacked RGBA layout with 32 bits of precision in each channel.

3.5.6.13.2. R32 G32 B32 A32 Definition

Definition Layout_R32_G32_B32_A32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_B32_A32_Channels R32_G32_B32_A32_NonEmpty R32_G32_B32_A32_FDiv8).

3.5.6.14. R32 G32 B32

1
An unpacked RGB layout with 32 bits of precision in each channel.

3.5.6.14.2. R32 G32 B32 Definition

Definition Layout_R32_G32_B32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_B32_Channels R32_G32_B32_NonEmpty R32_G32_B32_FDiv8).

3.5.6.15. R32 G32

1
An unpacked RG layout with 32 bits of precision in each channel.

3.5.6.15.2. R32 G32 Definition

Definition Layout_R32_G32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_Channels R32_G32_NonEmpty R32_G32_FDiv8).

3.5.6.16. R32

1
An unpacked R layout with 32 bits of precision in each channel.

3.5.6.16.2. R32 Definition

Definition Layout_R32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_Channels R32_NonEmpty R32_FDiv8).

3.5.6.17. R64 G64 B64 A64

1
An unpacked RGBA layout with 64 bits of precision in each channel.

3.5.6.17.2. R64 G64 B64 A64 Definition

Definition Layout_R64_G64_B64_A64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_B64_A64_Channels R64_G64_B64_A64_NonEmpty R64_G64_B64_A64_FDiv8).

3.5.6.18. R64 G64 B64

1
An unpacked RGB layout with 64 bits of precision in each channel.

3.5.6.18.2. R64 G64 B64 Definition

Definition Layout_R64_G64_B64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_B64_Channels R64_G64_B64_NonEmpty R64_G64_B64_FDiv8).

3.5.6.19. R64 G64

1
An unpacked RG layout with 64 bits of precision in each channel.

3.5.6.19.2. R64 G64 Definition

Definition Layout_R64_G64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_Channels R64_G64_NonEmpty R64_G64_FDiv8).

3.5.6.20. R64

1
An unpacked R layout with 64 bits of precision in each channel.

3.5.6.20.2. R64 Definition

Definition Layout_R64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_Channels R64_NonEmpty R64_FDiv8).

3.6. Color Spaces

1
The values in the n color channels of an image are interpreted as coordinates in an n-dimensional color space. A color space declaration indicates which color space is intended to be used.

3.6.2. Color Space

Inductive colorSpace : Set :=
  | CSLinear
  | CSsRGB
  | CSCustom : descriptor → colorSpace.
3
A value of CSLinear indicates that the color values should be interpreted as coordinates in a pure, conceptually linear color space.
4
A value of CSsRGB indicates that the color values should be interpreted as coordinates in the sRGB color space.
5
A value of CSCustom indicates that the color values should be interpreted as coordinates in a custom color space. Implementations are permitted to reject files containing unrecognized color spaces.
6
Color space declarations must use the following descriptors:

3.6.7. Color Space Description

Definition colorSpaceDescribe (c : colorSpace) : descriptor :=
  match c with
  | CSLinear   => "LINEAR"
  | CSsRGB     => "SRGB"
  | CSCustom d => d
  end.

3.6.8. Color Space Describable

Instance colorSpaceDescribable : describable colorSpace := {
  descriptorOf c := colorSpaceDescribe c
}.

3.7. Compression

3.7.1. Description

1
A compression declaration indicates that image data is compressed in a manner that is expected to interpreted directly by a consuming GPU. This is in contrast to super compression, where image data must be manually decompressed before it can be consumed by a GPU.

3.7.1.2. Compression Methods

Inductive compressionMethod : Set :=
  | CompressionUncompressed
  | CompressionBC1
  | CompressionBC2
  | CompressionBC3
  | CompressionBC4
  | CompressionBC5
  | CompressionBC6
  | CompressionBC7
  | CompressionETC1
  | CompressionETC2
  | CompressionEAC
  | CompressionASTC : nat → nat → compressionMethod
  | CompressionCustom :
    ∀ (d : descriptor)
      (blockSizeX : nat)
      (blockSizeY : nat)
      (identifier : nat)
      (align : nat), 0 < align → compressionMethod.
3
A value of CompressionUncompressed indicates that image data is not compressed.
4
A value of CompressionBC1 indicates that image data is compressed using BC1 compression (also known as DXT1 compression).
5
A value of CompressionBC2 indicates that image data is compressed using BC2 compression (also known as DXT3 compression).
6
A value of CompressionBC3 indicates that image data is compressed using BC3 compression (also known as DXT5 compression).
7
A value of CompressionBC4 indicates that image data is compressed using BC4 compression.
8
A value of CompressionBC5 indicates that image data is compressed using BC5 compression.
9
A value of CompressionBC6 indicates that image data is compressed using BC6 compression.
10
A value of CompressionBC7 indicates that image data is compressed using BC7 compression.
11
A value of CompressionETC1 indicates that image data is compressed using ETC1 compression.
12
A value of CompressionETC2 indicates that image data is compressed using ETC2 compression.
13
A value of CompressionEAC indicates that image data is compressed using EAC compression.
14
A value of CompressionASTC indicates that image data is compressed using ASTC compression.
15
A value of CompressionCustom indicates that image data is compressed using a method not known to this specification.
16
Compression declarations must use the following descriptors:

3.7.1.17. Compression Description

Definition compressionMethodDescriptor (c : compressionMethod) :=
  match c with
  | CompressionUncompressed       => "UNCOMPRESSED"
  | CompressionBC1                => "BC1"
  | CompressionBC2                => "BC2"
  | CompressionBC3                => "BC3"
  | CompressionBC4                => "BC4"
  | CompressionBC5                => "BC5"
  | CompressionBC6                => "BC6"
  | CompressionBC7                => "BC7"
  | CompressionETC1               => "ETC1"
  | CompressionETC2               => "ETC2"
  | CompressionEAC                => "EAC"
  | CompressionASTC _ _           => "ASTC"
  | CompressionCustom c _ _ _ _ _ => c
  end.

3.7.1.18. Compression Describable

Instance compressionMethodDescribable : describable compressionMethod := {
  descriptorOf c := compressionMethodDescriptor c
}.

3.7.2. Block Sizes

1
Compression methods have inherent block sizes that typically influence the required alignment in memory of compressed data.

3.7.2.2. Compression Block Size X

Definition compressionBlockSizeX (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 4
  | CompressionBC2                => 4
  | CompressionBC3                => 4
  | CompressionBC4                => 4
  | CompressionBC5                => 4
  | CompressionBC6                => 4
  | CompressionBC7                => 4
  | CompressionETC1               => 4
  | CompressionETC2               => 4
  | CompressionEAC                => 4
  | CompressionASTC x _           => x
  | CompressionCustom _ x _ _ _ _ => x
  end.

3.7.2.3. Compression Block Size Y

Definition compressionBlockSizeY (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 4
  | CompressionBC2                => 4
  | CompressionBC3                => 4
  | CompressionBC4                => 4
  | CompressionBC5                => 4
  | CompressionBC6                => 4
  | CompressionBC7                => 4
  | CompressionETC1               => 4
  | CompressionETC2               => 4
  | CompressionEAC                => 4
  | CompressionASTC _ y           => y
  | CompressionCustom _ _ y _ _ _ => y
  end.

3.7.2.4. Compression Block Alignment

Definition compressionBlockAlignment (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 8
  | CompressionBC2                => 16
  | CompressionBC3                => 16
  | CompressionBC4                => 8
  | CompressionBC5                => 16
  | CompressionBC6                => 16
  | CompressionBC7                => 16
  | CompressionETC1               => 16
  | CompressionETC2               => 16
  | CompressionEAC                => 16
  | CompressionASTC _ _           => 16
  | CompressionCustom _ _ _ _ a _ => a
  end.

3.7.3. Section Identifiers

1
Custom compression methods may require including extra metadata in order to allow the data to be decompressed. Compression methods may include a section identifier value indicating that consumers should look for a section with the given identifier to locate the metadata.

3.7.3.2. Compression Section Identifier

Definition compressionSectionIdentifier (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 0
  | CompressionBC2                => 0
  | CompressionBC3                => 0
  | CompressionBC4                => 0
  | CompressionBC5                => 0
  | CompressionBC6                => 0
  | CompressionBC7                => 0
  | CompressionETC1               => 0
  | CompressionETC2               => 0
  | CompressionEAC                => 0
  | CompressionASTC _ _           => 0
  | CompressionCustom _ _ _ i _ _ => i
  end.

3.8. Supercompression

3.8.1. Description

1
A super compression declaration indicates that image data is compressed in a manner that requires it to be decompressed before it can be consumed by a GPU for use. This is in contrast to compression, where GPUs are expected to consume compressed data directly.

3.8.1.2. Supercompression Methods

Inductive superCompressionMethod : Set :=
  | SuperCompressionUncompressed
  | SuperCompressionLZ4
  | SuperCompressionCustom : descriptor → nat → superCompressionMethod.
3
A value of SuperCompressionUncompressed indicates that image data is not compressed.
4
A value of SuperCompressionLZ4 indicates that image data is compressed using LZ4 compression.
5
A value of SuperCompressionCustom indicates that image data is compressed using a method not known to this specification.
6
Compression declarations must use the following descriptors:

3.8.1.7. Super Compression Description

Definition superCompressionMethodDescriptor (c : superCompressionMethod) :=
  match c with
  | SuperCompressionUncompressed => "UNCOMPRESSED"
  | SuperCompressionLZ4          => "LZ4"
  | SuperCompressionCustom c _   => c
  end.

3.8.1.8. Super Compression Describable

Instance superCompressionMethodDescribable : describable superCompressionMethod := {
  descriptorOf c := superCompressionMethodDescriptor c
}.

3.8.2. Section Identifiers

1
Custom super compression methods may require including extra metadata in order to allow the data to be decompressed. Super compression methods may include a section identifier value indicating that consumers should look for a section with the given identifier to locate the metadata.

3.8.2.2. Super Compression Section Identifier

Definition superCompressionSectionIdentifier (c : superCompressionMethod) : nat :=
  match c with
  | SuperCompressionUncompressed => 0
  | SuperCompressionLZ4          => 0
  | SuperCompressionCustom _ i   => i
  end.

3.9. Coordinate Systems

1
All images implicitly have a coordinate system such that the locations of pixels are specified relative to some origin point. For example, OpenGL's screen space is a coordinate system with the origin at the bottom left such that X coordinates increase rightwards and Y coordinates increase upwards. In contrast, Java2D's coordinate system has the origin at the top left such that X coordinates increase rightwards and Y coordinates increase downwards. Texture coordinates are typically expressed as a 3-tuple (R, S, T), where S is analogous to the X axis, T is analogous to the Y axis, and R is analogous to the Z axis. The R coordinate value is only present for 3D textures.

3.9.2. Texture Coordinates

Texture coordinates and origins.
3
The coordinate system of an image must match the coordinate system of the intended rendering system in order for the image to be rendered correctly. For example, taking an image that was intended for Java2D's system and rendering it directly in OpenGL will result in an image displaying upside down.
4
Textures in the calino package include descriptions of their coordinate systems. A coordinate system declaration comprises of three values that describe the orientations of the R, S, and T axes.

3.9.5. Coordinates R

Inductive coordinateAxisR : Set :=
  | AxisRIncreasingToward
  | AxisRIncreasingAway.
6
A value of AxisRIncreasingToward indicates that the R axis increases towards the viewer.
7
A value of AxisRIncreasingAway indicates that the R axis increases away from the viewer.

3.9.8. Coordinates S

Inductive coordinateAxisS : Set :=
  | AxisSIncreasingRight
  | AxisSIncreasingLeft.
9
A value of AxisSIncreasingRight indicates that the S axis increases rightwards.
10
A value of AxisSIncreasingLeft indicates that the S axis increases leftwards.

3.9.11. Coordinates T

Inductive coordinateAxisT : Set :=
  | AxisTIncreasingDown
  | AxisTIncreasingUp.
12
A value of AxisTIncreasingDown indicates that the S axis increases downwards.
13
A value of AxisTIncreasingUp indicates that the S axis increases upwards.

3.9.14. Coordinate System Values

Inductive coordinateSystem : Set :=
  CoordinateSystem : coordinateAxisR → coordinateAxisS → coordinateAxisT → coordinateSystem.
15
Coordinate system values must use the following descriptors:

3.9.16. Coordinates R Description

Definition coordinateAxisRDescribe (c : coordinateAxisR) : descriptor :=
  match c with
  | AxisRIncreasingToward => "RT"
  | AxisRIncreasingAway   => "RA"
  end.

3.9.17. Coordinates R Describable

Instance coordinateAxisRDescribable : describable coordinateAxisR := {
  descriptorOf c := coordinateAxisRDescribe c
}.

3.9.18. Coordinates S Description

Definition coordinateAxisSDescribe (c : coordinateAxisS) : descriptor :=
  match c with
  | AxisSIncreasingRight => "SR"
  | AxisSIncreasingLeft  => "SL"
  end.

3.9.19. Coordinates S Describable

Instance coordinateAxisSDescribable : describable coordinateAxisS := {
  descriptorOf c := coordinateAxisSDescribe c
}.

3.9.20. Coordinates T Description

Definition coordinateAxisTDescribe (c : coordinateAxisT) : descriptor :=
  match c with
  | AxisTIncreasingDown => "TD"
  | AxisTIncreasingUp   => "TU"
  end.

3.9.21. Coordinates T Describable

Instance coordinateAxisTDescribable : describable coordinateAxisT := {
  descriptorOf c := coordinateAxisTDescribe c
}.

3.9.22. Coordinate System Description

Definition coordinateSystemDescribe (c : coordinateSystem) : descriptor :=
  match c with
  | CoordinateSystem r s t =>
    descriptorOf r ++ ":" ++ descriptorOf s ++ ":" ++ descriptorOf t
  end.

3.9.23. Coordinate System Describable

Instance coordinateSystemDescribable : describable coordinateSystem := {
  descriptorOf c := coordinateSystemDescribe c
}.

3.10. Flags

1
A texture may have one or more boolean flags describing metadata that does not fit into any of the other categories of metadata included in calino texture files. A given flag may appear at most once in any given texture file.

3.10.2. Flag

Inductive flag : Set :=
  | FlagAlphaPremultiplied
  | FlagCustom : descriptor → flag.

3.10.3. Flags

Inductive flagSet : Set := {
  flags      : list flag;
  flagsNoDup : NoDup flags;
}.
4
A value of FlagAlphaPremultiplied indicates that the color channels of the image data have been multiplied by the value in the alpha channel of the image.
5
A value of FlagCustom indicates that the texture has flags not known to this specification.
6
Flags must use the following descriptors:

3.10.7. Flag Description

Definition flagDescribe (f : flag) : descriptor :=
  match f with
  | FlagAlphaPremultiplied => "ALPHA_PREMULTIPLIED"
  | FlagCustom d           => d
  end.

3.10.8. Flag Describable

Instance flagDescribable : describable flag := {
  descriptorOf f := flagDescribe f
}.

3.11. Image Information

1
An image information value aggregates all of the image metadata described in this specification.

3.11.2. Image Information

Record imageInfo : Set := ImageInfo {
  imageSize                   : imageSize3D;
  imageChannelsLayout         : channelLayoutDescription;
  imageChannelsType           : channelType;
  imageCompressionMethod      : compressionMethod;
  imageSuperCompressionMethod : superCompressionMethod;
  imageCoordinateSystem       : coordinateSystem;
  imageColorSpace             : colorSpace;
  imageFlags                  : flagSet;
  imageByteOrder              : byteOrder
}.

3.11.3. Image Size

Record imageSize3D : Set := ImageSize3D {
  sizeX     : nat;
  sizeY     : nat;
  sizeZ     : nat;
  sizeXnot0 : 0 ≠ sizeX;
  sizeYnot0 : 0 ≠ sizeY;
  sizeZnot0 : 0 ≠ sizeZ;
}.
4
The sizeX, sizeY, and sizeZ values declare the size of the image on the X, Y, and Z axes, respectively. All size values must be non-zero, and further restrictions may be placed on the size values by specific image types.
5
The texel block alignment is a value in octets to which image data is expected to be aligned. For compressed images, this is equal to the declared block alignment. For uncompressed images, this is equal to the total size of all of the channels in bits, divided by 8.

3.11.6. Texel Block Alignment

Definition imageInfoTexelBlockAlignment (i : imageInfo) :=
  let c := imageCompressionMethod i in
    match c with
    | CompressionUncompressed => channelLayoutDescriptionBits (imageChannelsLayout i) / 8
    | _                       => compressionBlockAlignment c
    end.

3.12. Mipmaps

1
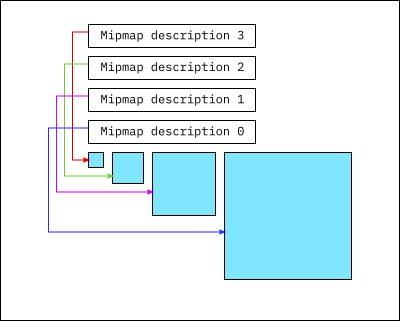
A 2D texture consists of a non-empty sequence of mipmaps. A sequence of mipmaps is a sequence of progressively scaled-down copies of a base image. Each mipmap level is numbered with the base image being at level 0 and the number of each subsequent level is the successor of the number of the previous level. The mipmap image at each level is half the width and height of the previous level.

3.12.2. Mipmaps Arrangement

Mipmaps Arrangement
3
A mipmap stores an offset indicating the start of the actual image data for the mipmap relative to the first octet of the first mipmap declaration. A mipmap also stores the compressed size and uncompressed size of the image data, along with a CRC32 checksum of the uncompressed data. A CRC32 value of 0 indicates that no checksum is available. For uncompressed data, the compressed and uncompressed sizes must equal the size of the uncompressed data.

3.12.4. MipMap

Inductive mipMap : Set := MipMap {
  mipMapLevel            : nat;
  mipMapOffset           : nat;
  mipMapSizeCompressed   : nat;
  mipMapSizeUncompressed : nat;
  mipMapCRC32            : nat
}.
5
Mipmap sequences are stored such that the data for the mipmap with the highest level is encountered first, whilst the data for the mipmap with level 0 is encountered last. This facilitates a common implementation pattern where textures are progressively streamed onto the GPU starting with the highest mipmap levels first. The proposition mipMapOffsetsSorted declares that, for a given mipmap m, the offset of m plus the compressed size of m, must be less than the offset of the next mipmap in the sequence.

3.12.6. MipMap Sequence Sorting

Inductive mipMapListIsSorted : list mipMap → Prop :=
  | MipsOne   : ∀ m, mipMapListIsSorted [m]
  | MipsCons  : ∀ mm0 mm1 mxs,
    mipMapLevel mm1 = S (mipMapLevel mm0) →
      mipMapListIsSorted (mm0 :: mxs) →
        mipMapListIsSorted (mm1 :: mm0 :: mxs).

3.12.7. MipMap Offsets Sorting

Inductive mipMapOffsetsSorted : list mipMap → Prop :=
  | MMSizeOne  : ∀ m, mipMapOffsetsSorted [m]
  | MMSizeCons : ∀ mm0 mm1 mxs,
    ((mipMapOffset mm1) + (mipMapSizeCompressed mm1)) < (mipMapOffset mm0) →
      mipMapOffsetsSorted (mm0 :: mxs) →
        mipMapOffsetsSorted (mm1 :: mm0 :: mxs).

3.12.8. MipMap Sequence

Inductive mipMapList : Set := MipMapList {
  mipMaps            : list mipMap;
  mipMapListSorted   : mipMapListIsSorted mipMaps;
  mipMapOffsetSorted : mipMapOffsetsSorted mipMaps;
}.
9
Given a base image of size (sizeX, sizeY), the size of the mipmap at level n is given by (sizeX / 2ⁿ, sizeY / 2ⁿ). Mipmap images are required to be of a size >= 2 on the X and Y axes. Note that this restriction does not apply to the base image; a base image with a size of 1 on any axis simply cannot have anything but a level 0 mipmap.

3.12.10. MipMap Size

Inductive mipMapImageSize : Set := MipMapImageSize {
  mmSizeX      : nat;
  mmSizeY      : nat;
  mmSizeXRange : 1 < mmSizeX;
  mmSizeYRange : 1 < mmSizeY;
}.

3.12.11. MipMap Size Calculation

Definition mipMapSize
  (level      : nat)
  (imageSize  : imageSize3D)
  (levelRange : 0 < level)
: option mipMapImageSize :=
  let sx := (sizeX imageSize) / 2 ^ level in
  let sy := (sizeY imageSize) / 2 ^ level in
    match (Nat.ltb_spec0 1 sx, Nat.ltb_spec0 1 sy) with
    | (ReflectT _ xt, ReflectT _ yt) => Some (MipMapImageSize sx sy xt yt)
    | (_, _)                         => None
    end.
12
The total size required to hold the image data for all mipmaps is effectively equal to the offset of the largest mipmap, plus the compressed size of the mipmap, rounded up to the required alignment of the image data.

3.12.13. MipMap Data Size (Aux)

Fixpoint mipMapImageDataSizeTotalAux (m : list mipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => (mipMapOffset x) + (mipMapSizeCompressed x)
  | (x :: xs) => mipMapImageDataSizeTotalAux xs
  end.

3.12.14. MipMap Data Size

Definition mipMapImageDataSizeTotal (m : mipMapList) : nat :=
  mipMapImageDataSizeTotalAux (mipMaps m).
15
The uncompressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.
16
The compressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.

3.13. Array Mipmaps

1
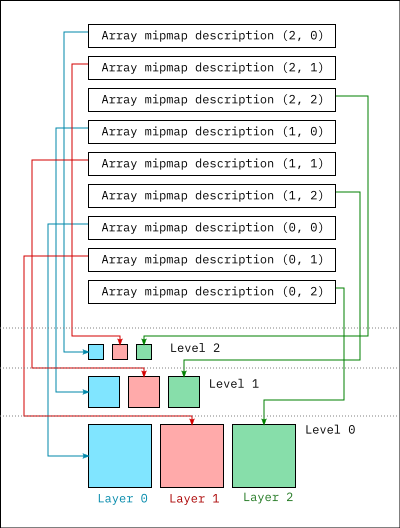
A 2D array texture consists of a non-empty sequence of array mipmaps. Array mipmaps are very similar to mipmaps with the primary difference that, for a texture with n array layers, each array mipmap level stores a sequence of n images of the same size. This facilitates a common implementation pattern where textures are progressively streamed onto the GPU starting with the array layers in the highest mipmap levels first.

3.13.2. Array Mipmaps Arrangement

Array Mipmaps Arrangement
3
An array mipmap is uniquely identified with a level and a layer.

3.13.4. ArrayMipMap Index

Inductive arrayMipMapIndexT : Set := ArrayMipMapIndex {
  arrayMipMapLevel : nat;
  arrayMipMapLayer : nat;
}.
5
An array mipmap stores an offset indicating the start of the actual image data for the mipmap relative to the first octet of the first mipmap declaration. An array mipmap also stores the compressed size and uncompressed size of the image data, along with a CRC32 checksum of the uncompressed data. A CRC32 value of 0 indicates that no checksum is available. For uncompressed data, the compressed and uncompressed sizes must equal the size of the uncompressed data.

3.13.6. ArrayMipMap

Inductive arrayMipMap : Set := ArrayMipMap {
  arrayMipMapIndex            : arrayMipMapIndexT;
  arrayMipMapOffset           : nat;
  arrayMipMapSizeCompressed   : nat;
  arrayMipMapSizeUncompressed : nat;
  arrayMipMapCRC32            : nat
}.
7
The number of layers present in an array mipmap must equal the sizeZ value defined in the image info, and it follows that all array mipmaps must contain the same number of layers.

3.13.8. ArrayMipMap Layer Count For Level

Fixpoint arrayMipMapLayerCountForLevel
  (level : nat)
  (m     : list arrayMipMap)
: nat :=
  match m with
  | []        => 0
  | (x :: xs) =>
    match Nat.eq_dec (arrayMipMapLevel (arrayMipMapIndex x)) level with
    | left _  => 1 + (arrayMipMapLayerCountForLevel level xs)
    | right _ => (arrayMipMapLayerCountForLevel level xs)
    end
  end.

3.13.9. ArrayMipMap Levels

Definition arrayMipMapLevels (m : list arrayMipMap) : list nat :=
  nodup Nat.eq_dec (map (λ k, arrayMipMapLevel (arrayMipMapIndex k)) m).

3.13.10. ArrayMipMap Levels Count Equality

Definition arrayMipMapsHaveSameLayers : (list arrayMipMap) → nat → nat → Prop :=
  λ m level0 level1,
    In level0 (arrayMipMapLevels m) →
      In level1 (arrayMipMapLevels m) →
        arrayMipMapLayerCountForLevel level0 m = arrayMipMapLayerCountForLevel level1 m.
11
Array mipmap sequences are stored such that the data for the mipmap with the highest level is encountered first, whilst the data for the mipmap with level 0 is encountered last. Within a given level, images are stored such that the data for layer 0 is encountered first, whilst the data for the highest layer is encountered last. The proposition arrayMipMapIndexOrd formally specifies the ordering for level/layer pairs, whilst the arrayMipMapIndicesSorted proposition formally specifies the conditions under which lists of level/layer pairs are considered to be ordered.

3.13.12. ArrayMipMap Index Ordering

Inductive arrayMipMapIndexOrd : arrayMipMapIndexT → arrayMipMapIndexT → Prop :=
  | AMMIOrdEq : ∀ i0 i1,
    i0 = i1 → arrayMipMapIndexOrd i0 i1
  | AMMIOrdLevelEq : ∀ i0 i1,
    arrayMipMapLevel i0 = arrayMipMapLevel i1 →
      arrayMipMapLayer i0 < arrayMipMapLayer i1 →
        arrayMipMapIndexOrd i0 i1
  | AMIIOrdLevelLt : ∀ i0 i1,
    arrayMipMapLevel i1 < arrayMipMapLevel i0 →
      arrayMipMapIndexOrd i0 i1.

3.13.13. ArrayMipMap Index List Sorted

Inductive arrayMipMapIndicesSorted : list arrayMipMapIndexT → Prop :=
  | AMMIOne  : ∀ m, arrayMipMapIndicesSorted [m]
  | AMMICons : ∀ mmx mmy mxs,
    arrayMipMapIndexOrd mmx mmy →
      arrayMipMapIndicesSorted (mmy :: mxs) →
        arrayMipMapIndicesSorted (mmx :: mmy :: mxs).

3.13.14. ArrayMipMap Sequence

Inductive arrayMipMapList : Set := ArrayMipMapList {
  arrayMipMaps                : list arrayMipMap;
  arrayMipMapIndicesAreSorted : arrayMipMapIndicesSorted (map arrayMipMapIndex arrayMipMaps);
  arrayMipMapOffsetAreSorted  : arrayMipMapOffsetsSorted arrayMipMaps;
  arrayMipMapSameLayers       : ∀ level0 level1, arrayMipMapsHaveSameLayers arrayMipMaps level0 level1
}.
15
The proposition arrayMipMapOffsetsSorted declares that, for a given array mipmap m, the offset of m plus the compressed size of m, must be less than the offset of the next mipmap in the sequence.

3.13.16. ArrayMipMap Offsets Sorted

Inductive arrayMipMapOffsetsSorted : list arrayMipMap → Prop :=
  | AMMSizeOne  : ∀ m, arrayMipMapOffsetsSorted [m]
  | AMMSizeCons : ∀ mm0 mm1 mxs,
    ((arrayMipMapOffset mm1) + (arrayMipMapSizeCompressed mm1)) < (arrayMipMapOffset mm0) →
      arrayMipMapOffsetsSorted (mm0 :: mxs) →
        arrayMipMapOffsetsSorted (mm1 :: mm0 :: mxs).
17
Given a base image of size (sizeX, sizeY), the size of the mipmap at level n is given by (sizeX / 2ⁿ, sizeY / 2ⁿ). Mipmap images are required to be of a size >= 2 on the X and Y axes. Note that this restriction does not apply to the base image; a base image with a size of 1 on any axis simply cannot have anything but a level 0 mipmap.

3.13.18. Array MipMap Size

Inductive arrayMipMapImageSize : Set := ArrayMipMapImageSize {
  ammSizeX      : nat;
  ammSizeY      : nat;
  ammSizeXRange : 1 < ammSizeX;
  ammSizeYRange : 1 < ammSizeY;
}.

3.13.19. Array MipMap Size Calculation

Definition arrayMipMapSize
  (level      : nat)
  (imageSize  : imageSize3D)
  (levelRange : 0 < level)
: option arrayMipMapImageSize :=
  let sx  := (sizeX imageSize) / 2 ^ level  in
  let sy  := (sizeY imageSize) / 2 ^ level  in
    match (Nat.ltb_spec0 1 sx, Nat.ltb_spec0 1 sy) with
    | (ReflectT _ xt, ReflectT _ yt) => Some (ArrayMipMapImageSize sx sy xt yt)
    | (_, _)                         => None
    end.
20
The total size required to hold the image data for all mipmaps is effectively equal to the offset of the largest mipmap, plus the compressed size of the mipmap, rounded up to the required alignment of the image data.

3.13.21. Array MipMap Data Size (Aux)

Fixpoint arrayMipMapImageDataSizeTotalAux (m : list arrayMipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => (arrayMipMapOffset x) + (arrayMipMapSizeCompressed x)
  | (x :: xs) => arrayMipMapImageDataSizeTotalAux xs
  end.

3.13.22. Array MipMap Data Size

Definition arrayMipMapImageDataSizeTotal (m : arrayMipMapList) : nat :=
  arrayMipMapImageDataSizeTotalAux (arrayMipMaps m).
23
The uncompressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.
24
The compressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.

3.14. Cube Mipmaps

1
A cube texture consists of a non-empty sequence of cube mipmaps. Cube mipmaps are very similar to mipmaps with the primary difference that each cube mipmap level stores a sequence of 6 images of the same size representing the faces of the cube.

3.14.2. Cube Mipmaps Arrangement

Cube Mipmaps Arrangement
3
Cube textures define an axis-aligned cube, with each of the six images in any given mipmap level defining each of the six axis-aligned cube faces. For example, when we refer to the positive X face of the cube, we are referring to the face of the cube that points towards positive infinity on the X axis. Each cube map face stores an offset indicating the start of the actual image data for the face relative to the first octet of the first mipmap declaration. A face also stores the compressed size and uncompressed size of the image data, along with a CRC32 checksum of the uncompressed data. A CRC32 value of 0 indicates that no checksum is available. For uncompressed data, the compressed and uncompressed sizes must equal the size of the uncompressed data.

3.14.4. CubeMap Face

Inductive cubeMapFace : Set := CubeMapFace {
  cubeFaceOffset           : nat;
  cubeFaceSizeCompressed   : nat;
  cubeFaceSizeUncompressed : nat;
  cubeFaceCRC32            : nat
}.
5
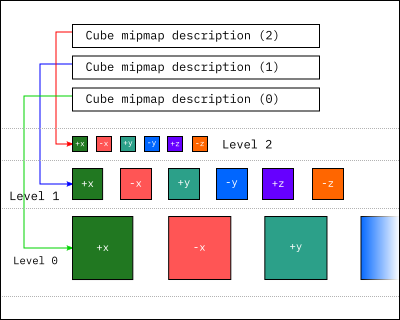
A single cube mipmap level stores the sequence of six cube faces in the following order: x-positive, x-negative, y-positive, y-negative, z-positive, z-negative. Cube mipmap sequences are stored such that the data for the mipmap with the highest level is encountered first, whilst the data for the mipmap with level 0 is encountered last. This facilitates a common implementation pattern where textures are progressively streamed onto the GPU starting with the highest mipmap levels first. The proposition cubeMipMapListIsSorted declares the conditions that indicate that a sequence of cube mipmap levels is correctly ordered.

3.14.6. CubeMap Level

Inductive cubeMipMap : Set := CubeMipMap {
  cubeMapLevel     : nat;
  cubeMapFaceXPos  : cubeMapFace;
  cubeMapFaceXNeg  : cubeMapFace;
  cubeMapFaceYPos  : cubeMapFace;
  cubeMapFaceYNeg  : cubeMapFace;
  cubeMapFaceZPos  : cubeMapFace;
  cubeMapFaceZNeg  : cubeMapFace
}.

3.14.7. CubeMap Ordering

Inductive cubeMipMapListIsSorted : list cubeMipMap → Prop :=
  | CubeOne   : ∀ m, cubeMipMapListIsSorted [m]
  | CubeCons  : ∀ mm0 mm1 mxs,
    cubeMapLevel mm1 = S (cubeMapLevel mm0) →
      cubeMipMapListIsSorted (mm0 :: mxs) →
        cubeMipMapListIsSorted (mm1 :: mm0 :: mxs).
8
The extent of a cube face is defined as the offset of the face plus the compressed size of the face. The extent of a cube mipmap level is the extent of the last face in the sequence (the z-negative face). This extent is effectively the smallest region that can contain all six faces of a level. The proposition cubeOffsetsSorted declares that, for a given cube mipmap m, the extents of the faces of m must be ordered correctly, and must be less than the offset of the first face of the next mipmap in the sequence.

3.14.9. CubeMap Extent

Definition cubeFaceExtent (f : cubeMapFace) : nat :=
  cubeFaceOffset f + cubeFaceSizeCompressed f.

3.14.10. CubeMap Offset Ordering

Inductive cubeOffsetsSorted : list cubeMipMap → Prop :=
  | CMMSizeOne  : ∀ m,
    cubeFaceExtent (cubeMapFaceXPos m) < cubeFaceOffset (cubeMapFaceXNeg m) →
    cubeFaceExtent (cubeMapFaceXNeg m) < cubeFaceOffset (cubeMapFaceYPos m) →
    cubeFaceExtent (cubeMapFaceYPos m) < cubeFaceOffset (cubeMapFaceYNeg m) →
    cubeFaceExtent (cubeMapFaceYNeg m) < cubeFaceOffset (cubeMapFaceZPos m) →
    cubeFaceExtent (cubeMapFaceZPos m) < cubeFaceOffset (cubeMapFaceZNeg m) →
      cubeOffsetsSorted [m]
  | CMMSizeCons : ∀ mm0 mm1 mxs,
    cubeFaceExtent (cubeMapFaceZNeg mm1) < cubeFaceOffset (cubeMapFaceXPos mm0) →
      cubeOffsetsSorted (mm0 :: mxs) →
        cubeOffsetsSorted (mm1 :: mm0 :: mxs).
11
Given a base image of size (sizeX, sizeY), the size of the mipmap at level n is given by (sizeX / 2ⁿ, sizeY / 2ⁿ). Mipmap images are required to be of a size >= 2 on the X and Y axes. Note that this restriction does not apply to the base image; a base image with a size of 1 on any axis simply cannot have anything but a level 0 mipmap.
12
The total size required to hold the image data for all mipmaps is effectively equal to the extent of the largest mipmap rounded up to the required alignment of the image data.

3.14.13. CubeMap Size (Aux)

Fixpoint cubeMipMapImageDataSizeTotalAux (m : list cubeMipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => cubeFaceExtent (cubeMapFaceZNeg x)
  | (x :: xs) => cubeMipMapImageDataSizeTotalAux xs
  end.

3.14.14. CubeMap Size

Definition cubeMipMapImageDataSizeTotal (m : cubeMipMapList) : nat :=
  cubeMipMapImageDataSizeTotalAux (cubeMipMaps m).
15
The uncompressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.
16
The compressed size of a mipmap should be non-zero. This property is implicit in the definitions above; images must be of a non-zero width and height, and there are no channel layouts where the sizes of the channels sum to zero.

3.15. Metadata

1
A texture file can have associated free-form metadata. This is often used to, for example, express authorship information and indicate which tools were used to produce a given file. The metadata supported directly by calino is in the form of UTF-8 encoded keys and values. Metadata that requires more structure than this can be provided by custom sections that will be ignored by software that does not know how to interpret them.

3.15.2. Metadata Value

Inductive metadataValue : Set := MetadataValue {
  mKey   : string;
  mValue : string
}.

3.15.3. Metadata

Inductive metadata : Set := Metadata {
  mValues : list metadataValue
}.
4
Conceptually, metadata is structured as a function from keys to non-empty lists of values; the values associated with multiple occurrences of a given key are expected to be combined into a list of values for the given key by consumers.

3.16. Textures

3.16.1. Textures

1
An texture is a 2D texture, an array texture, or a cube texture.

3.16.1.2. Texture

Inductive texture : Set :=
  | TTexture2D    : texture2d → texture
  | TTextureArray : textureArray → texture
  | TTextureCube  : textureCube → texture.

3.16.2. 2D Texture

1
A 2D texture aggregates image information and a sequence of mipmaps for a single two-dimensional texture.
2
2D textures must have sizeZ values equal to 1.

3.16.2.3. 2D Texture

Inductive texture2d : Set := Texture2D {
  i2dInfo    : imageInfo;
  i2dMipMaps : mipMapList;
  i2dSize    : 1 = imageSizeZ i2dInfo
}.

3.16.3. Array Texture

1
An array texture aggregates image information and a sequence of array mipmaps for a single two-dimensional array texture.
2
Array textures must have sizeZ values equal to the number of array layers in the texture.

3.16.3.3. Array Texture

Inductive textureArray : Set := TextureArray {
  iaInfo    : imageInfo;
  iaMipMaps : arrayMipMapList;
  iaSize    : 1 <= imageSizeZ iaInfo
}.

3.16.4. 3D Texture

1
3D textures are not yet specified.

3.16.5. Cube Texture

1
A cube texture aggregates image information and a sequence of cube mipmaps for a single cube texture.
2
Cube textures must have sizeZ values equal to 1.

3.16.5.3. Cube Image

Inductive textureCube : Set := TextureCube {
  icubeInfo    : imageInfo;
  icubeMipMaps : cubeMipMapList;
  icubeSize    : 1 = imageSizeZ icubeInfo
}.

4. The Calino Binary Encoding

4.1. Binary Expressions

4.1.1. Overview

1
The calino texture file format has a strict and easy-to-parse binary encoding, defined in terms of a small binary expression language. Terms in this binary expression language, when evaluated, produce streams of octets that are concatenated together to produce the final output file. This section of the specification defines the expression language, whilst subsequent sections describe how the semantic structures given in the model are mapped to binary expressions.

4.1.2. Expressions

1
A term in the binary expression language is described by the following inductive type:

4.1.2.2. Binary Expression

Inductive binaryExp : Set :=
    | BiU32     : nat → binaryExp
    | BiU64     : nat → binaryExp
    | BiBytes   : list byte → binaryExp
    | BiUTF8    : list byte → binaryExp
    | BiArray   : list binaryExp → binaryExp
    | BiReserve : nat → binaryExp
    | BiRecord  : list (string * binaryExp) → binaryExp.
3
An expression BiU32 n represents an unsigned 32-bit integer n.
4
An expression BiU64 n represents an unsigned 64-bit integer n.
5
An expression BiBytes xs represents an octet array. Octet arrays are prefixed with an unsigned 32-bit integer value denoting their size in octets, not including any padding. Octet arrays are unconditionally padded with unsigned 8-bit values such that the total size of the array including padding is evenly divisible by 4.
6
An expression BiUTF8 xs represents a UTF-8 encoded string. Strings are prefixed with an unsigned 32-bit integer value denoting their encoded size in octets, not including any padding. Strings are unconditionally padded with unsigned 8-bit values such that the total size of the string including padding is evenly divisible by 4.
7
An expression BiArray xs represents an array of binary expressions xs. Arrays are prefixed with an unsigned 32-bit integer value denoting the number of array elements present.
8
An expression BiReserve n represents a block of reserved data of n octets in length. Data is unconditionally padded with unsigned 8-bit values such that the total size of the string including padding is evenly divisible by 4.
9
An expression BiRecord fs represents a sequence of named expression values. Intuitively, they can be considered to be fields of a record type. The number of fields is not present in the resulting encoded octet stream, and the names of fields are not included either. Consumers are expected to know, from reading this specification, when to expect a record type in a stream.
10
All of the possible forms of binary expression have an encoded size that is a multiple of 4. The sizes of each encoded expression form are given by binarySize:

4.1.2.11. Binary Expression Sizes

Fixpoint binarySize (b : binaryExp) : nat :=
  match b with
  | BiU32 _     => 4
  | BiU64 _     => 8
  | BiBytes s   => 4 + asMultipleOf4 (length s)
  | BiUTF8 s    => 4 + asMultipleOf4 (length s)
  | BiArray f   => 4 + fold_right plus 0 (map binarySize f)
  | BiReserve s => asMultipleOf4 s
  | BiRecord f  => fold_right plus 0 (map (binarySize ∘ snd) f)
  end.

4.1.2.12. Binary Expression Sizes (multiple of)

Definition asMultipleOf (size q : nat) (Hnz : 0 ≠ q) : nat :=
  let r := size / q in
    match Nat.ltb_spec0 r q with
    | ReflectT _ _ => (r + 1) * q
    | ReflectF _ _ => r * q
    end.

4.1.2.13. Binary Expression Size Theorem

Theorem binarySizeMultiple4 : ∀ b, binarySize (b) mod 4 = 0.
Proof.
  (* Proof omitted for brevity; see Binary.v for proofs. *)
Qed.
14
This specification text makes use of a convenient abbreviation function, binarySizePadded16, to concisely denote the size of binary expressions padded to a size that is a multiple of 16, as well as a partial application of asMultipleOf fixed to a multiple of 4:

4.1.2.15. Binary Expression Size Padded 16

Definition binarySizePadded16 (b : binaryExp) : nat :=
  asMultipleOf16 (binarySize b).

4.1.2.16. asMultipleOf4

Definition asMultipleOf4 (size : nat) : nat :=
  asMultipleOf size 4 p0not4.
17
Binary expressions are encoded as streams of streamE values:

4.1.2.18. Stream Elements

Inductive streamE : Set :=
  | Vu64 : nat → streamE
  | Vu32 : nat → streamE
  | Vu8  : nat → streamE.
19
An expression Vu64 n represents an unsigned 64-bit integer in big-endian order.
20
An expression Vu32 n represents an unsigned 32-bit integer in big-endian order.
21
An expression Vu8 n represents an unsigned 8-bit integer.
22
A given binary expression is transformed to a stream of octets using the following encoding rules:

4.1.2.23. Binary Expression Encoding

Fixpoint binaryEval (b : binaryExp) : list streamE :=
  match b with
  | BiU32 k     => [Vu32 k]
  | BiU64 k     => [Vu64 k]
  | BiBytes s   => (Vu32 (length s)) :: (binaryEvalPaddedBytes s 4 p0not4)
  | BiUTF8 s    => (Vu32 (length s)) :: (binaryEvalPaddedBytes s 4 p0not4)
  | BiArray f   => (Vu32 (length f)) :: concat (map binaryEval f)
  | BiReserve s => repeat (Vu8 0) (asMultipleOf4 s)
  | BiRecord f  => concat (map (binaryEval ∘ snd) f)
  end.

4.1.2.24. Binary Expression Encoding (Padding)

Definition binaryEvalPaddedBytes
  (b     : list byte)
  (align : nat)
  (Hneq  : 0 ≠ align)
: list streamE :=
  let vremaining := length b mod align in
    match vremaining with
    | 0 => map u8byte b
    | _ => map u8byte (b ++ repeat x00 (align - vremaining))
    end.
25
Informally, a stream s is well-formed if exactly one of the following conditions holds:

4.1.2.26. Well-Formed Stream (Informal rules)

  • s is empty.
  • s consists of a single 64-bit integer.
  • s consists of a single 32-bit integer.
  • s consists of a sequence of n 8-bit integers, where n is evenly divisible by 4.
  • s is the concatenation of a well-formed stream t and a well-formed stream u.
27
The rules for well-formedness correspond to the following proposition:

4.1.2.28. Well-Formed Stream

Inductive streamWellFormed : list streamE → Prop :=
  | BEPEmpty : streamWellFormed []
  | BEPVu64 : ∀ k, streamWellFormed [Vu64 k]
  | BEPVu32 : ∀ k, streamWellFormed [Vu32 k]
  | BEPVu8s : ∀ es, Forall streamEIsU8 es → length (es) mod 4 = 0 → streamWellFormed es
  | BEPAppend : ∀ xs ys, streamWellFormed xs → streamWellFormed ys → streamWellFormed (xs ++ ys).
29
The binary expression encoding rules produce well-formed streams. It follows that any well-formed stream has a size that is evenly divisible by 4.

4.1.2.30. Binary Expression Encoding Well-Formed

Theorem binaryEvalStreamsWellFormed : ∀ b,
  streamWellFormed (binaryEval b).
Proof.
  (* Proof omitted for brevity; see Binary.v for proofs. *)
Qed.

4.1.2.31. Binary Expression Encoding Size Divisible

Theorem streamsWellFormedDivisible4 : ∀ es,
  streamWellFormed es → streamSize es mod 4 = 0.
Proof.
  (* Proof omitted for brevity; see Binary.v for proofs. *)
Qed.

4.2. File Header

1
All calino texture files begin with the following fixed length header:

4.2.2. File Header

Definition binaryExpFileHeader : binaryExp := BiRecord [
  ("id",           u64 0x89434C4E0D0A1A0A);
  ("versionMajor", u32 1);
  ("versionMinor", u32 0)
].
3
The id field must always be set to the 64-bit unsigned big-endian value 0x89434C4E0D0A1A0A.
4
The versionMajor field must be set to 1 for files targeting this version of the specification.
5
The versionMinor field must be set to 0 for files targeting this version of the specification.

4.3. Sections

1
calino texture files are structured as a sequence of explicitly sized sections. A section consists of a 64-bit identifier i, a 64-bit size value s, followed by s octets of data, followed by zero or more octets of padding such that the next section will begin on a 16 octet boundary. Consumers that do not recognize the identifier of a given section can simply skip the section by seeking forwards by s octets to find the next section.
2
The first section in a calino texture should be an image information section.
3
Following an image information section, calino texture files must contain exactly one of any of the various texture data sections.
4
calino texture files must end with exactly one End section.
5
Sections should start at offsets that are evenly divisible by 16.
6
The following standard sections are defined by this version of the specification:

4.3.7. Standard Sections

Identifier Description
0x434C4E49494E464F Image information.
0x434C4E5F49324421 Image data for 2D textures.
0x434C4E5F41525221 Image data for array textures.
0x434C4E5F43554245 Image data for cube textures.
0x434C4E5F4D455441 Key/value metadata.
0x434C4E5F454E4421 File terminator.

4.4. Image Information

4.4.1. Description

1
Image information values are translated to binary expressions as follows:

4.4.1.2. Image Information Encoding

Definition binaryExpImageInfo (i : imageInfo) : binaryExp := BiRecord [
  ("sizeX",            u32 (imageSizeX i));
  ("sizeY",            u32 (imageSizeY i));
  ("sizeZ",            u32 (imageSizeZ i));
  ("channelsLayout",   utf8 (descriptorOf (imageChannelsLayout i)));
  ("channelsType",     utf8 (descriptorOf (imageChannelsType i)));
  ("compression",      binaryExpCompression (imageCompressionMethod i));
  ("superCompression", binaryExpSuperCompression (imageSuperCompressionMethod i));
  ("coordinateSystem", utf8 (descriptorOf (imageCoordinateSystem i)));
  ("colorSpace",       utf8 (descriptorOf (imageColorSpace i)));
  ("flags",            BiArray (map (utf8 ∘ descriptorOf) (imageFlagSet i)));
  ("byteOrder",        utf8 (descriptorOf (imageByteOrder i)))
].
3
Compression declarations are translated to binary expressions as follows:

4.4.1.4. Compression Encoding

Definition binaryExpCompression (c : compressionMethod) : binaryExp := BiRecord [
  ("descriptor",        utf8 (descriptorOf c));
  ("sectionIdentifier", u64 (compressionSectionIdentifier c));
  ("blockSizeX",        u32 (compressionBlockSizeX c));
  ("blockSizeY",        u32 (compressionBlockSizeY c));
  ("blockAlignment",    u32 (compressionBlockAlignment c))
].
5
Super compression declarations are translated to binary expressions as follows:

4.4.1.6. Super Compression Encoding

Definition binaryExpSuperCompression (c : superCompressionMethod) : binaryExp := BiRecord [
  ("descriptor",        utf8 (descriptorOf c));
  ("sectionIdentifier", u64 (superCompressionSectionIdentifier c))
].
7
Image information must be encoded into a section with identifier 0x434C4E49494E464F as follows:

4.4.1.8. Image Information Section

Definition binaryExpImageInfoSection (i : imageInfo) : binaryExp := BiRecord [
  ("id",   u64 0x434C4E49494E464F);
  ("size", u64 (binarySizePadded16 (binaryExpImageInfo i)));
  ("data", binaryExpImageInfo i)
].

4.4.2. Cardinality

1
An image information section can appear in a calino texture file at most once.

4.5. 2D Textures

4.5.1. Description

1
2D texture values are translated to binary expressions as follows:

4.5.1.2. MipMap Encoding

Definition binaryExpMipMap (m : mipMap) : binaryExp := BiRecord [
  ("mipMapLevel",            u32 (mipMapLevel m));
  ("mipMapDataOffset",       u64 (mipMapOffset m));
  ("mipMapSizeUncompressed", u64 (mipMapSizeUncompressed m));
  ("mipMapSizeCompressed",   u64 (mipMapSizeCompressed m));
  ("mipMapCRC32",            u32 (mipMapCRC32 m))
].

4.5.1.3. MipMaps Encoding

Definition binaryExpMipMaps (m : mipMapList) : binaryExp :=
  BiArray (map binaryExpMipMap (mipMaps m)).

4.5.1.4. Image 2D Encoding

Definition binaryExpImage2D
  (i : imageInfo)
  (m : mipMapList)
: binaryExp :=
  let imageDataStart := mipMapOffset (mipMapFirst m) in
  let encMips        := binaryExpMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := mipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("mipMaps", encMips);
      ("mipPad",  BiReserve encMipsPad);
      ("mipData", BiReserve imageSize16)
    ].
5
Informally, an array of mipmap descriptions are serialized, followed by any required padding to reach the offset value declared by the first mipmap, followed by the image data for each mipmap in the order specified by the mipmap descriptions.
6
2D textures must be encoded into a section with identifier 0x434C4E5F49324421 as follows:

4.5.1.7. Image 2D Section

Definition binaryExpImage2DSection
  (i : imageInfo)
  (m : mipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F49324421);
  ("size", u64 (binarySizePadded16 (binaryExpImage2D i m)));
  ("data", binaryExpImage2D i m)
].

4.5.2. Cardinality

1
A 2D texture section can appear in a calino texture file at most once.

4.6. Array Textures

4.6.1. Description

1
Array texture values are translated to binary expressions as follows:

4.6.1.2. Array MipMap Encoding

Definition binaryExpArrayMipMap (m : arrayMipMap) : binaryExp := BiRecord [
  ("arrayMipMapLevel",            u32 (arrayMipMapLevel (arrayMipMapIndex m)));
  ("arrayMipMapLayer",            u32 (arrayMipMapLayer (arrayMipMapIndex m)));
  ("arrayMipMapDataOffset",       u64 (arrayMipMapOffset m));
  ("arrayMipMapSizeUncompressed", u64 (arrayMipMapSizeUncompressed m));
  ("arrayMipMapSizeCompressed",   u64 (arrayMipMapSizeCompressed m));
  ("arrayMipMapCRC32",            u32 (arrayMipMapCRC32 m))
].

4.6.1.3. Array MipMaps Encoding

Definition binaryExpArrayMipMaps (m : arrayMipMapList) : binaryExp :=
  BiArray (map binaryExpArrayMipMap (arrayMipMaps m)).

4.6.1.4. Array Image Encoding

Definition binaryExpImageArray
  (i : imageInfo)
  (m : arrayMipMapList)
: binaryExp :=
  let imageDataStart := arrayMipMapOffset (arrayMipMapFirst m) in
  let encMips        := binaryExpArrayMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := arrayMipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("arrayMipMaps", encMips);
      ("arrayMipPad",  BiReserve encMipsPad);
      ("arrayMipData", BiReserve imageSize16)
    ].
5
Informally, an array of array mipmap descriptions are serialized, followed by any required padding to reach the offset value declared by the first mipmap, followed by the image data for each mipmap in the order specified by the mipmap descriptions.
6
Array textures must be encoded into a section with identifier 0x434C4E5F41525221 as follows:

4.6.1.7. Array Image Section

Definition binaryExpImageArraySection
  (i : imageInfo)
  (m : arrayMipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F41525221);
  ("size", u64 (binarySizePadded16 (binaryExpImageArray i m)));
  ("data", binaryExpImageArray i m)
].

4.6.2. Cardinality

1
An array texture section can appear in a calino texture file at most once.

4.7. Cube Textures

4.7.1. Description

1
Cube texture values are translated to binary expressions as follows:

4.7.1.2. Cube MipMap Face Encoding

Definition binaryExpCubeMipMapFace (m : cubeMapFace) : binaryExp := BiRecord [
  ("cubeFaceDataOffset",       u64 (cubeFaceOffset m));
  ("cubeFaceSizeUncompressed", u64 (cubeFaceSizeUncompressed m));
  ("cubeFaceSizeCompressed",   u64 (cubeFaceSizeCompressed m));
  ("cubeFaceCRC32",            u32 (cubeFaceCRC32 m))
].

4.7.1.3. Cube MipMap Encoding

Definition binaryExpCubeMipMap (m : cubeMipMap) : binaryExp := BiRecord [
  ("cubeMipMapLevel",    u32 (cubeMapLevel m));
  ("cubeMipMapFacePosX", binaryExpCubeMipMapFace (cubeMapFaceXPos m));
  ("cubeMipMapFaceNegX", binaryExpCubeMipMapFace (cubeMapFaceXNeg m));
  ("cubeMipMapFacePosY", binaryExpCubeMipMapFace (cubeMapFaceYPos m));
  ("cubeMipMapFaceNegY", binaryExpCubeMipMapFace (cubeMapFaceYNeg m));
  ("cubeMipMapFacePosZ", binaryExpCubeMipMapFace (cubeMapFaceZPos m));
  ("cubeMipMapFaceNegZ", binaryExpCubeMipMapFace (cubeMapFaceZNeg m))
].

4.7.1.4. Cube MipMaps Encoding

Definition binaryExpCubeMipMaps (m : cubeMipMapList) : binaryExp :=
  BiArray (map binaryExpCubeMipMap (cubeMipMaps m)).

4.7.1.5. Image Cube Encoding

Definition binaryExpImageCubeMap
  (i : imageInfo)
  (m : cubeMipMapList)
: binaryExp :=
  let imageDataStart := cubeFaceOffset (cubeMapFaceXPos (cubeMipMapsFirst m)) in
  let encMips        := binaryExpCubeMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := cubeMipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("cubeMipMaps", encMips);
      ("cubeMipPad",  BiReserve encMipsPad);
      ("cubeMipData", BiReserve imageSize16)
    ].
6
Informally, an array of mipmap descriptions are serialized, followed by any required padding to reach the offset value declared by the first mipmap, followed by the image data for each mipmap in the order specified by the mipmap descriptions.
7
Cube textures must be encoded into a section with identifier 0x434C4E5F43554245 as follows:

4.7.1.8. Image Cube Section

Definition binaryExpImageCubeSection
  (i : imageInfo)
  (m : cubeMipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F43554245);
  ("size", u64 (binarySizePadded16 (binaryExpImageCubeMap i m)));
  ("data", binaryExpImageCubeMap i m)
].

4.7.2. Cardinality

1
A cube texture section can appear in a calino texture file at most once.

4.8. Metadata

4.8.1. Description

1
Metadata values are translated to binary expressions as follows:

4.8.1.2. Metadata Value Encoding

Definition binaryExpMetadataValue (m : metadataValue) : binaryExp := BiRecord [
  ("key",   utf8 (mKey m));
  ("value", utf8 (mValue m))
].

4.8.1.3. Metadata Encoding

Definition binaryExpMetadata (m : metadata) : binaryExp :=
  BiArray (map binaryExpMetadataValue (mValues m)).
4
Metadata must be encoded into a section with identifier 0x434C4E5F4D455441 as follows:

4.8.1.5. Metadata Section

Definition binaryExpMetadataSection (m : metadata) : binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F4D455441);
  ("size", u64 (binarySizePadded16 (binaryExpMetadata m)));
  ("data", binaryExpMetadata m)
].

4.8.2. Cardinality

1
A metadata section can appear in a calino texture file at most once.

4.9. End

4.9.1. Description

1
calino texture files must end with exactly one End section, which has the identifier 0x434C4E5F454E4421 and must be of size 0.
2
End sections are encoded as follows:

4.9.1.3. End Encoding

Definition binaryEndSection : binaryExp := BiRecord [
  ("id",   u64 0x434c4e5f454e4421);
  ("size", u64 0)
].
4
There should be no trailing data in the texture file after the End section.

4.9.2. Cardinality

1
An End section must appear in a calino texture file exactly once, and must be the last section present in the file.

4.10. Examples

1
A metadata section containing the value Metadata [MetadataValue "K0" "VAL0"; MetadataValue "KEY1" "VAL1"] will be encoded as the following sequence of octets:

4.10.2. Example Metadata

43 4C 4E 5F  4D 45 54 41                ; Identifier 0x434C4E49494E464F
00 00 00 00  00 00 00 30                ; Section is 48 bytes

00 00 00 02                             ; Size of metadata array is 2
00 00 00 02                             ; Size of first key is 2
4B 30 00 00                             ; Key is "K0" plus padding octets
00 00 00 04                             ; Size of first value is 4
56 41 4C 30                             ; Value is "VAL0", no padding required
00 00 00 04                             ; Size of second key is 4
4B 45 59 31                             ; Key is "KEY1", no padding required
00 00 00 04                             ; Size of second value is 4
56 41 4C 31                             ; Value is "VAL1", no padding required

00 00 00 00  00 00 00 00  00 00 00 00   ; 12 padding octets, so the size of the
                                        ; section is a multiple of 16

5. Sources

1
The full sources for the Coq/Gallina model underlying this specification are included here.

5.2. Calino/Alignment.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Strings.String.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Init.Byte.
Require Import Coq.Bool.Bool.
Require Import Coq.Program.Basics.
Require Import Coq.Unicode.Utf8_core.

Definition asMultipleOf (size q : nat) (Hnz : 0 ≠ q) : nat :=
  let r := size / q in
    match Nat.ltb_spec0 r q with
    | ReflectT _ _ => (r + 1) * q
    | ReflectF _ _ => r * q
    end.

Lemma p0not4 : 0 ≠ 4.
Proof. discriminate. Qed.

Lemma p0not16 : 0 ≠ 16.
Proof. discriminate. Qed.

Definition asMultipleOf4 (size : nat) : nat :=
  asMultipleOf size 4 p0not4.

Definition asMultipleOf16 (size : nat) : nat :=
  asMultipleOf size 16 p0not16.

Lemma asMultipleOfMod : ∀ s q (Hneq : 0 ≠ q), (asMultipleOf s q Hneq) mod q = 0.
Proof.
  intros s q Hneq.
  unfold asMultipleOf.
  destruct (Nat.ltb_spec0 (s / q) q) as [Hlt|H1].
  - apply (Nat.mod_mul (s / q + 1) q (Nat.neq_sym _ _ Hneq)).
  - apply (Nat.mod_mul (s / q) q (Nat.neq_sym _ _ Hneq)).
Qed.

5.3. Calino/ArrayMipMap.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Bool.Bool.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.ImageSize.

Import ListNotations.

Inductive arrayMipMapIndexT : Set := ArrayMipMapIndex {
  arrayMipMapLevel : nat;
  arrayMipMapLayer : nat;
}.

Inductive arrayMipMapIndexOrd : arrayMipMapIndexT → arrayMipMapIndexT → Prop :=
  | AMMIOrdEq : ∀ i0 i1,
    i0 = i1 → arrayMipMapIndexOrd i0 i1
  | AMMIOrdLevelEq : ∀ i0 i1,
    arrayMipMapLevel i0 = arrayMipMapLevel i1 →
      arrayMipMapLayer i0 < arrayMipMapLayer i1 →
        arrayMipMapIndexOrd i0 i1
  | AMIIOrdLevelLt : ∀ i0 i1,
    arrayMipMapLevel i1 < arrayMipMapLevel i0 →
      arrayMipMapIndexOrd i0 i1.

Inductive arrayMipMapIndicesSorted : list arrayMipMapIndexT → Prop :=
  | AMMIOne  : ∀ m, arrayMipMapIndicesSorted [m]
  | AMMICons : ∀ mmx mmy mxs,
    arrayMipMapIndexOrd mmx mmy →
      arrayMipMapIndicesSorted (mmy :: mxs) →
        arrayMipMapIndicesSorted (mmx :: mmy :: mxs).

Inductive arrayMipMap : Set := ArrayMipMap {
  arrayMipMapIndex            : arrayMipMapIndexT;
  arrayMipMapOffset           : nat;
  arrayMipMapSizeCompressed   : nat;
  arrayMipMapSizeUncompressed : nat;
  arrayMipMapCRC32            : nat
}.

Inductive arrayMipMapOffsetsSorted : list arrayMipMap → Prop :=
  | AMMSizeOne  : ∀ m, arrayMipMapOffsetsSorted [m]
  | AMMSizeCons : ∀ mm0 mm1 mxs,
    ((arrayMipMapOffset mm1) + (arrayMipMapSizeCompressed mm1)) < (arrayMipMapOffset mm0) →
      arrayMipMapOffsetsSorted (mm0 :: mxs) →
        arrayMipMapOffsetsSorted (mm1 :: mm0 :: mxs).

Fixpoint arrayMipMapLayerCountForLevel
  (level : nat)
  (m     : list arrayMipMap)
: nat :=
  match m with
  | []        => 0
  | (x :: xs) =>
    match Nat.eq_dec (arrayMipMapLevel (arrayMipMapIndex x)) level with
    | left _  => 1 + (arrayMipMapLayerCountForLevel level xs)
    | right _ => (arrayMipMapLayerCountForLevel level xs)
    end
  end.

Definition arrayMipMapLevels (m : list arrayMipMap) : list nat :=
  nodup Nat.eq_dec (map (λ k, arrayMipMapLevel (arrayMipMapIndex k)) m).

Definition arrayMipMapsHaveSameLayers : (list arrayMipMap) → nat → nat → Prop :=
  λ m level0 level1,
    In level0 (arrayMipMapLevels m) →
      In level1 (arrayMipMapLevels m) →
        arrayMipMapLayerCountForLevel level0 m = arrayMipMapLayerCountForLevel level1 m.

Inductive arrayMipMapList : Set := ArrayMipMapList {
  arrayMipMaps                : list arrayMipMap;
  arrayMipMapIndicesAreSorted : arrayMipMapIndicesSorted (map arrayMipMapIndex arrayMipMaps);
  arrayMipMapOffsetAreSorted  : arrayMipMapOffsetsSorted arrayMipMaps;
  arrayMipMapSameLayers       : ∀ level0 level1, arrayMipMapsHaveSameLayers arrayMipMaps level0 level1
}.

Inductive arrayMipMapImageSize : Set := ArrayMipMapImageSize {
  ammSizeX      : nat;
  ammSizeY      : nat;
  ammSizeXRange : 1 < ammSizeX;
  ammSizeYRange : 1 < ammSizeY;
}.

Lemma arrayMipMapsNonEmpty : ∀ (m : arrayMipMapList),
  [] ≠ arrayMipMaps m.
Proof.
  intros m.
  destruct (arrayMipMapOffsetAreSorted m).
  - discriminate.
  - discriminate.
Qed.

Definition arrayMipMapFirst (m : arrayMipMapList) : arrayMipMap.
Proof.
  assert ([] ≠ arrayMipMaps m) as Hneq by (apply (arrayMipMapsNonEmpty)).
  destruct (arrayMipMaps m) eqn:Hm.
  - contradiction.
  - exact a.
Defined.

Lemma lt_neq : ∀ n, 0 ≠ n ↔ 0 < n.
Proof.
  intros n.
  constructor.
  - intro Hneq.
    induction n as [|k].
    -- unfold not in Hneq.
       assert (0 = 0) as Heq by reflexivity.
       contradiction.
    -- apply (Nat.lt_0_succ k).
  - intro Hneq.
    induction n as [|k].
    -- inversion Hneq.
    -- discriminate.
Qed.

Lemma lt_neq_0 : ∀ n, 0 ≠ n → 0 < n.
Proof.
  intros n Hneq.
  rewrite <- lt_neq; trivial.
Qed.

Lemma lt_neq_1 : ∀ n, 0 < n → 0 ≠ n.
Proof.
  intros n Hneq.
  rewrite lt_neq; trivial.
Qed.

Definition arrayMipMapSize
  (level      : nat)
  (imageSize  : imageSize3D)
  (levelRange : 0 < level)
: option arrayMipMapImageSize :=
  let sx  := (sizeX imageSize) / 2 ^ level  in
  let sy  := (sizeY imageSize) / 2 ^ level  in
    match (Nat.ltb_spec0 1 sx, Nat.ltb_spec0 1 sy) with
    | (ReflectT _ xt, ReflectT _ yt) => Some (ArrayMipMapImageSize sx sy xt yt)
    | (_, _)                         => None
    end.

Fixpoint arrayMipMapImageDataSizeTotalAux (m : list arrayMipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => (arrayMipMapOffset x) + (arrayMipMapSizeCompressed x)
  | (x :: xs) => arrayMipMapImageDataSizeTotalAux xs
  end.

Definition arrayMipMapImageDataSizeTotal (m : arrayMipMapList) : nat :=
  arrayMipMapImageDataSizeTotalAux (arrayMipMaps m).

Example exampleArrayMipMapsIndices := [
  (ArrayMipMapIndex 2 0);
  (ArrayMipMapIndex 2 1);
  (ArrayMipMapIndex 2 2);
  (ArrayMipMapIndex 1 0);
  (ArrayMipMapIndex 1 1);
  (ArrayMipMapIndex 1 2);
  (ArrayMipMapIndex 0 0);
  (ArrayMipMapIndex 0 1);
  (ArrayMipMapIndex 0 2)
].

Example exampleArrayMipMaps :=
  map (λ i, ArrayMipMap i 0 0 0 0) exampleArrayMipMapsIndices.

Example exampleArrayMipMapIndicesSorted : arrayMipMapIndicesSorted exampleArrayMipMapsIndices.
Proof.
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMICons. { apply AMIIOrdLevelLt. compute; constructor. }
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMICons. { apply AMIIOrdLevelLt. compute; constructor. }
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMICons. { apply AMMIOrdLevelEq. reflexivity. compute; constructor. }
  apply AMMIOne.
Qed.

Example exampleArrayMipMapsHaveSameLayers0 : arrayMipMapLayerCountForLevel 0 exampleArrayMipMaps = 3.
Proof. reflexivity. Qed.
Example exampleArrayMipMapsHaveSameLayers1 : arrayMipMapLayerCountForLevel 1 exampleArrayMipMaps = 3.
Proof. reflexivity. Qed.
Example exampleArrayMipMapsHaveSameLayers2 : arrayMipMapLayerCountForLevel 2 exampleArrayMipMaps = 3.
Proof. reflexivity. Qed.

Example exampleArrayMipMapsLevel : ∀ n, In n (arrayMipMapLevels exampleArrayMipMaps) →
  n = 0 \/ n = 1 \/ n = 2.
Proof.
  intros n.
  simpl.
  intros H.
  destruct H; auto.
  destruct H; auto.
  destruct H; auto.
  contradiction H.
Qed.

Example exampleArrayMipMapsHaveSameLayers : ∀ level0 level1, arrayMipMapsHaveSameLayers exampleArrayMipMaps level0 level1.
Proof.
  intros level0 level1.
  unfold arrayMipMapsHaveSameLayers.
  intros H_In0 H_In1.
  assert (level0 = 0 ∨ level0 = 1 ∨ level0 = 2) as Hl0 by (apply (exampleArrayMipMapsLevel level0 H_In0)).
  assert (level1 = 0 ∨ level1 = 1 ∨ level1 = 2) as Hl1 by (apply (exampleArrayMipMapsLevel level1 H_In1)).
  destruct Hl0 as [Heq0|Heq0]. {
    destruct Hl1 as [Heq1|Heq1]. {
      rewrite Heq0.
      rewrite Heq1.
      reflexivity.
    }
    destruct Heq1 as [Heq1_0|Heq1_0]. {
      rewrite Heq0.
      rewrite Heq1_0.
      reflexivity.
    }
    rewrite Heq0.
    rewrite Heq1_0.
    reflexivity.
  }
  destruct Heq0 as [Heq0_0|Heq0_0]. {
    rewrite Heq0_0.
    destruct Hl1 as [Heq1|Heq1]. {
      rewrite Heq1.
      reflexivity.
    }
    destruct Heq1 as [Heq1_0|Heq1_0]. {
      rewrite Heq1_0.
      reflexivity.
    }
    rewrite Heq1_0.
    reflexivity.
  }
  destruct Hl1 as [Heq1|Heq1]. {
    rewrite Heq0_0.
    rewrite Heq1.
    reflexivity.
  }
  destruct Heq1 as [Heq1_0|Heq1_0]. {
    rewrite Heq0_0.
    rewrite Heq1_0.
    reflexivity.
  }
  rewrite Heq0_0.
  rewrite Heq1_0.
  reflexivity.
Qed.

5.4. Calino/Binary.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Strings.String.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Init.Byte.
Require Import Coq.Bool.Bool.
Require Import Coq.Program.Basics.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Alignment.
Require Import Calino.Metadata.
Require Import Calino.ArrayMipMap.
Require Import Calino.CubeMipMap.
Require Import Calino.MipMap.
Require Import Calino.ImageInfo.
Require Import Calino.Divisible8.
Require Import Calino.StringUtility.
Require Import Calino.Descriptor.
Require Import Calino.ChannelDescription.
Require Import Calino.ChannelSemantic.
Require Import Calino.ChannelType.
Require Import Calino.Compression.
Require Import Calino.SuperCompression.
Require Import Calino.ColorSpace.
Require Import Calino.Flag.
Require Import Calino.ByteOrder.
Require Import Calino.CoordinateSystem.
Require Import Calino.ImageSize.

Import ListNotations.

Open Scope program_scope.
Open Scope string_scope.

Set Mangle Names.

Inductive streamE : Set :=
  | Vu64 : nat → streamE
  | Vu32 : nat → streamE
  | Vu8  : nat → streamE.

Definition u8byte : byte → streamE :=
  Vu8 ∘ Byte.to_nat.

Definition streamEIsU8 (e : streamE) : Prop :=
  match e with
  | Vu64 _ => False
  | Vu32 _ => False
  | Vu8  _ => True
  end.

Inductive streamWellFormed : list streamE → Prop :=
  | BEPEmpty : streamWellFormed []
  | BEPVu64 : ∀ k, streamWellFormed [Vu64 k]
  | BEPVu32 : ∀ k, streamWellFormed [Vu32 k]
  | BEPVu8s : ∀ es, Forall streamEIsU8 es → length (es) mod 4 = 0 → streamWellFormed es
  | BEPAppend : ∀ xs ys, streamWellFormed xs → streamWellFormed ys → streamWellFormed (xs ++ ys).

Definition streamElementSize (s : streamE) : nat :=
  match s with
  | Vu64 _ => 8
  | Vu32 _ => 4
  | Vu8  _ => 1
  end.

Definition streamSize (s : list streamE) : nat :=
  fold_right plus 0 (map streamElementSize s).

Section binaryExpressions.

  Local Unset Elimination Schemes.

  Inductive binaryExp : Set :=
    | BiU32     : nat → binaryExp
    | BiU64     : nat → binaryExp
    | BiBytes   : list byte → binaryExp
    | BiUTF8    : list byte → binaryExp
    | BiArray   : list binaryExp → binaryExp
    | BiReserve : nat → binaryExp
    | BiRecord  : list (string * binaryExp) → binaryExp.

  Section binaryExp_rect.
    Variable P             : binaryExp → Type.
    Variable P_list        : list binaryExp → Type.
    Hypothesis P_nil       : P_list [].
    Hypothesis P_cons      : ∀ x xs, P x → P_list xs → P_list (x :: xs).
    Hypothesis P_BiU32     : ∀ x, P (BiU32 x).
    Hypothesis P_BiU64     : ∀ x, P (BiU64 x).
    Hypothesis P_BiBytes   : ∀ bs, P (BiBytes bs).
    Hypothesis P_BiUTF8    : ∀ bs, P (BiUTF8 bs).
    Hypothesis P_BiArray   : ∀ bs, P_list bs → P (BiArray bs).
    Hypothesis P_BiReserve : ∀ x, P (BiReserve x).
    Hypothesis P_BiRecord  : ∀ fs, P_list (map snd fs) → P (BiRecord fs).

    Fixpoint binaryExp_rect (b : binaryExp) : P b :=
      let
        fix expForAll (xs : list binaryExp) : P_list xs :=
          match xs as rxs return (P_list rxs) with
          | []        => @P_nil
          | (y :: ys) => @P_cons y ys (binaryExp_rect y) (expForAll ys)
          end
      in let
        fix forAllSnd (fs : list (string * binaryExp)) : P_list (map snd fs) :=
          match fs as rf return P_list (map snd rf) with
          | []             => @P_nil
          | ((_, y) :: ys) => @P_cons y (map snd ys) (binaryExp_rect y) (forAllSnd ys)
          end
      in
        match b with
        | BiU32 c     => P_BiU32 c
        | BiU64 c     => P_BiU64 c
        | BiBytes bs  => P_BiBytes bs
        | BiUTF8 bs   => P_BiUTF8 bs
        | BiArray es  => P_BiArray es (expForAll es)
        | BiReserve c => P_BiReserve c
        | BiRecord fs => P_BiRecord fs (forAllSnd fs)
        end.

  End binaryExp_rect.

  Section binaryExp_ind.
    Variable P             : binaryExp → Prop.
    Hypothesis P_BiU32     : ∀ x, P (BiU32 x).
    Hypothesis P_BiU64     : ∀ x, P (BiU64 x).
    Hypothesis P_BiBytes   : ∀ bs, P (BiBytes bs).
    Hypothesis P_BiUTF8    : ∀ bs, P (BiUTF8 bs).
    Hypothesis P_BiArray   : ∀ bs, Forall P bs → P (BiArray bs).
    Hypothesis P_BiReserve : ∀ x, P (BiReserve x).
    Hypothesis P_BiRecord  : ∀ fs, Forall P (map snd fs) → P (BiRecord fs).

    Definition binaryExp_ind (b : binaryExp) : P b :=
      binaryExp_rect
        P
        (List.Forall P)
        (List.Forall_nil _)
        (λ x xs Px Pxs, List.Forall_cons _ Px Pxs)
        P_BiU32
        P_BiU64
        P_BiBytes
        P_BiUTF8
        P_BiArray
        P_BiReserve
        P_BiRecord
        b.

  End binaryExp_ind.
End binaryExpressions.

Fixpoint binarySize (b : binaryExp) : nat :=
  match b with
  | BiU32 _     => 4
  | BiU64 _     => 8
  | BiBytes s   => 4 + asMultipleOf4 (length s)
  | BiUTF8 s    => 4 + asMultipleOf4 (length s)
  | BiArray f   => 4 + fold_right plus 0 (map binarySize f)
  | BiReserve s => asMultipleOf4 s
  | BiRecord f  => fold_right plus 0 (map (binarySize ∘ snd) f)
  end.

Definition binaryEvalPaddedBytes
  (b     : list byte)
  (align : nat)
  (Hneq  : 0 ≠ align)
: list streamE :=
  let vremaining := length b mod align in
    match vremaining with
    | 0 => map u8byte b
    | _ => map u8byte (b ++ repeat x00 (align - vremaining))
    end.

Fixpoint binaryEval (b : binaryExp) : list streamE :=
  match b with
  | BiU32 k     => [Vu32 k]
  | BiU64 k     => [Vu64 k]
  | BiBytes s   => (Vu32 (length s)) :: (binaryEvalPaddedBytes s 4 p0not4)
  | BiUTF8 s    => (Vu32 (length s)) :: (binaryEvalPaddedBytes s 4 p0not4)
  | BiArray f   => (Vu32 (length f)) :: concat (map binaryEval f)
  | BiReserve s => repeat (Vu8 0) (asMultipleOf4 s)
  | BiRecord f  => concat (map (binaryEval ∘ snd) f)
  end.

Definition binarySizePadded16 (b : binaryExp) : nat :=
  asMultipleOf16 (binarySize b).

Definition utf8 (s : string) : binaryExp :=
  BiUTF8 (list_byte_of_string s).

Definition u32 := BiU32.
Definition u64 := BiU64.

Definition binaryExpMipMap (m : mipMap) : binaryExp := BiRecord [
  ("mipMapLevel",            u32 (mipMapLevel m));
  ("mipMapDataOffset",       u64 (mipMapOffset m));
  ("mipMapSizeUncompressed", u64 (mipMapSizeUncompressed m));
  ("mipMapSizeCompressed",   u64 (mipMapSizeCompressed m));
  ("mipMapCRC32",            u32 (mipMapCRC32 m))
].

Remark binaryExpMipMapSize : ∀ m, binarySize (binaryExpMipMap m) = 32.
Proof. reflexivity. Qed.

Definition binaryExpMipMaps (m : mipMapList) : binaryExp :=
  BiArray (map binaryExpMipMap (mipMaps m)).

Definition binaryExpImage2D
  (i : imageInfo)
  (m : mipMapList)
: binaryExp :=
  let imageDataStart := mipMapOffset (mipMapFirst m) in
  let encMips        := binaryExpMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := mipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("mipMaps", encMips);
      ("mipPad",  BiReserve encMipsPad);
      ("mipData", BiReserve imageSize16)
    ].

Definition binaryExpImage2DSection
  (i : imageInfo)
  (m : mipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F49324421);
  ("size", u64 (binarySizePadded16 (binaryExpImage2D i m)));
  ("data", binaryExpImage2D i m)
].

Definition binaryExpArrayMipMap (m : arrayMipMap) : binaryExp := BiRecord [
  ("arrayMipMapLevel",            u32 (arrayMipMapLevel (arrayMipMapIndex m)));
  ("arrayMipMapLayer",            u32 (arrayMipMapLayer (arrayMipMapIndex m)));
  ("arrayMipMapDataOffset",       u64 (arrayMipMapOffset m));
  ("arrayMipMapSizeUncompressed", u64 (arrayMipMapSizeUncompressed m));
  ("arrayMipMapSizeCompressed",   u64 (arrayMipMapSizeCompressed m));
  ("arrayMipMapCRC32",            u32 (arrayMipMapCRC32 m))
].

Remark binaryExpArrayMipMapSize : ∀ m, binarySize (binaryExpArrayMipMap m) = 36.
Proof. reflexivity. Qed.

Definition binaryExpArrayMipMaps (m : arrayMipMapList) : binaryExp :=
  BiArray (map binaryExpArrayMipMap (arrayMipMaps m)).

Definition binaryExpImageArray
  (i : imageInfo)
  (m : arrayMipMapList)
: binaryExp :=
  let imageDataStart := arrayMipMapOffset (arrayMipMapFirst m) in
  let encMips        := binaryExpArrayMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := arrayMipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("arrayMipMaps", encMips);
      ("arrayMipPad",  BiReserve encMipsPad);
      ("arrayMipData", BiReserve imageSize16)
    ].

Definition binaryExpImageArraySection
  (i : imageInfo)
  (m : arrayMipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F41525221);
  ("size", u64 (binarySizePadded16 (binaryExpImageArray i m)));
  ("data", binaryExpImageArray i m)
].

Definition binaryExpCubeMipMapFace (m : cubeMapFace) : binaryExp := BiRecord [
  ("cubeFaceDataOffset",       u64 (cubeFaceOffset m));
  ("cubeFaceSizeUncompressed", u64 (cubeFaceSizeUncompressed m));
  ("cubeFaceSizeCompressed",   u64 (cubeFaceSizeCompressed m));
  ("cubeFaceCRC32",            u32 (cubeFaceCRC32 m))
].

Remark binaryExpCubeMipMapFaceSize : ∀ m, binarySize (binaryExpCubeMipMapFace m) = 28.
Proof. reflexivity. Qed.

Definition binaryExpCubeMipMap (m : cubeMipMap) : binaryExp := BiRecord [
  ("cubeMipMapLevel",    u32 (cubeMapLevel m));
  ("cubeMipMapFacePosX", binaryExpCubeMipMapFace (cubeMapFaceXPos m));
  ("cubeMipMapFaceNegX", binaryExpCubeMipMapFace (cubeMapFaceXNeg m));
  ("cubeMipMapFacePosY", binaryExpCubeMipMapFace (cubeMapFaceYPos m));
  ("cubeMipMapFaceNegY", binaryExpCubeMipMapFace (cubeMapFaceYNeg m));
  ("cubeMipMapFacePosZ", binaryExpCubeMipMapFace (cubeMapFaceZPos m));
  ("cubeMipMapFaceNegZ", binaryExpCubeMipMapFace (cubeMapFaceZNeg m))
].

Remark binaryExpCubeMipMapSize : ∀ m, binarySize (binaryExpCubeMipMap m) = 172.
Proof. reflexivity. Qed.

Definition binaryExpCubeMipMaps (m : cubeMipMapList) : binaryExp :=
  BiArray (map binaryExpCubeMipMap (cubeMipMaps m)).

Definition binaryExpImageCubeMap
  (i : imageInfo)
  (m : cubeMipMapList)
: binaryExp :=
  let imageDataStart := cubeFaceOffset (cubeMapFaceXPos (cubeMipMapsFirst m)) in
  let encMips        := binaryExpCubeMipMaps m in
  let encMipsSize    := binarySize encMips in
  let encMipsPad     := imageDataStart - encMipsSize in
  let imageSize      := cubeMipMapImageDataSizeTotal m in
  let imageSize16    := asMultipleOf16 imageSize in
    BiRecord [
      ("cubeMipMaps", encMips);
      ("cubeMipPad",  BiReserve encMipsPad);
      ("cubeMipData", BiReserve imageSize16)
    ].

Definition binaryExpImageCubeSection
  (i : imageInfo)
  (m : cubeMipMapList)
: binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F43554245);
  ("size", u64 (binarySizePadded16 (binaryExpImageCubeMap i m)));
  ("data", binaryExpImageCubeMap i m)
].

Definition binaryExpCompression (c : compressionMethod) : binaryExp := BiRecord [
  ("descriptor",        utf8 (descriptorOf c));
  ("sectionIdentifier", u64 (compressionSectionIdentifier c));
  ("blockSizeX",        u32 (compressionBlockSizeX c));
  ("blockSizeY",        u32 (compressionBlockSizeY c));
  ("blockAlignment",    u32 (compressionBlockAlignment c))
].

Definition binaryExpSuperCompression (c : superCompressionMethod) : binaryExp := BiRecord [
  ("descriptor",        utf8 (descriptorOf c));
  ("sectionIdentifier", u64 (superCompressionSectionIdentifier c))
].

Definition binaryExpImageInfo (i : imageInfo) : binaryExp := BiRecord [
  ("sizeX",            u32 (imageSizeX i));
  ("sizeY",            u32 (imageSizeY i));
  ("sizeZ",            u32 (imageSizeZ i));
  ("channelsLayout",   utf8 (descriptorOf (imageChannelsLayout i)));
  ("channelsType",     utf8 (descriptorOf (imageChannelsType i)));
  ("compression",      binaryExpCompression (imageCompressionMethod i));
  ("superCompression", binaryExpSuperCompression (imageSuperCompressionMethod i));
  ("coordinateSystem", utf8 (descriptorOf (imageCoordinateSystem i)));
  ("colorSpace",       utf8 (descriptorOf (imageColorSpace i)));
  ("flags",            BiArray (map (utf8 ∘ descriptorOf) (imageFlagSet i)));
  ("byteOrder",        utf8 (descriptorOf (imageByteOrder i)))
].

Definition binaryExpFileHeader : binaryExp := BiRecord [
  ("id",           u64 0x89434C4E0D0A1A0A);
  ("versionMajor", u32 1);
  ("versionMinor", u32 0)
].

Definition binaryExpImageInfoSection (i : imageInfo) : binaryExp := BiRecord [
  ("id",   u64 0x434C4E49494E464F);
  ("size", u64 (binarySizePadded16 (binaryExpImageInfo i)));
  ("data", binaryExpImageInfo i)
].

Definition binaryExpMetadataValue (m : metadataValue) : binaryExp := BiRecord [
  ("key",   utf8 (mKey m));
  ("value", utf8 (mValue m))
].

Definition binaryExpMetadata (m : metadata) : binaryExp :=
  BiArray (map binaryExpMetadataValue (mValues m)).

Definition binaryExpMetadataSection (m : metadata) : binaryExp := BiRecord [
  ("id",   u64 0x434C4E5F4D455441);
  ("size", u64 (binarySizePadded16 (binaryExpMetadata m)));
  ("data", binaryExpMetadata m)
].

Definition binaryEndSection : binaryExp := BiRecord [
  ("id",   u64 0x434c4e5f454e4421);
  ("size", u64 0)
].

Lemma fold_right_add_cons : ∀ x xs,
  x + fold_right plus 0 xs = fold_right plus 0 (x :: xs).
Proof. reflexivity. Qed.

Lemma forall_map_binarySize : ∀ es,
  Forall (λ b : binaryExp, binarySize b mod 4 = 0) es
    ↔ Forall (λ n, n mod 4 = 0) (map binarySize es).
Proof.
  intros es.
  induction es.
  constructor.
  - rewrite Forall_map.
    intros H. trivial.
  - rewrite Forall_map.
    intros H. trivial.
  - rewrite Forall_map.
    constructor.
    intros H; trivial.
    intros H; trivial.
Qed.

Theorem binarySizeMultiple4 : ∀ b, binarySize (b) mod 4 = 0.
Proof.
  intros b.
  induction b as [Hbu32|Hbu64|Hbbyte|Hbutf|xs HFA|Hbuns|xs HFF] using binaryExp_ind.
  (* U32 values are of size 4 *)
  - reflexivity.
  (* U64 values are of size 8 *)
  - reflexivity.
  (* Byte array values are rounded up to a multiple of 4 and prefixed with 4 *)
  - unfold binarySize.
    unfold asMultipleOf4.
    remember (asMultipleOf (Datatypes.length Hbbyte) 4 p0not4) as size eqn:Heqsize.
    rewrite Nat.add_comm.
    rewrite <- (Nat.add_mod_idemp_l size 4 4 (Nat.neq_sym _ _ p0not4)).
    assert (size mod 4 = 0) as Hm0. {
      rewrite Heqsize.
      apply (asMultipleOfMod (Datatypes.length Hbbyte) 4 (p0not4)).
    }
    rewrite Hm0.
    reflexivity.
  (* UTF-8 values are rounded up to a multiple of 4 and prefixed with 4 *)
  - unfold binarySize.
    unfold asMultipleOf4.
    remember (asMultipleOf (Datatypes.length Hbutf) 4 p0not4) as size eqn:Heqsize.
    rewrite Nat.add_comm.
    rewrite <- (Nat.add_mod_idemp_l size 4 4 (Nat.neq_sym _ _ p0not4)).
    assert (size mod 4 = 0) as Hm0. {
      rewrite Heqsize.
      apply (asMultipleOfMod (Datatypes.length Hbutf) 4 (p0not4)).
    }
    rewrite Hm0.
    reflexivity.
  (* Each element of an array is a multiple of 4, so the entire array is too. *)
  - unfold binarySize.
    fold binarySize.
    induction xs as [|y ys HforAllInd].
    -- reflexivity.
    -- assert (fold_right add 0 (map binarySize (y :: ys)) mod 4 = 0) as HfoldEq. {
         apply (@divisibilityNFoldPlus 4 (map binarySize (y :: ys))).
         discriminate.
         rewrite <- forall_map_binarySize.
         exact HFA.
       }
       rewrite map_cons.
       rewrite map_cons in HfoldEq.
       assert (4 mod 4 = 0) as H4mod40 by (reflexivity).
       assert (0 ≠ 4) as H0n4 by (discriminate).
       apply (divisiblityNAdd 4 (fold_right add 0 (binarySize y :: map binarySize ys)) 4 H0n4 H4mod40 HfoldEq).
  (* Unspecified values are rounded up. *)
  - unfold binarySize.
    unfold asMultipleOf4.
    rewrite asMultipleOfMod.
    reflexivity.
  (* Each element of an record is a multiple of 4, so the entire record is too. *)
  - unfold binarySize.
    fold binarySize.
    induction xs as [|y ys HforAllInd].
    -- reflexivity.
    -- rewrite map_cons.
       rewrite map_cons in HFF.
       rewrite <- fold_right_add_cons.
       apply divisiblityNAdd.
       discriminate.
       apply (Forall_inv HFF).
       apply HforAllInd.
       apply (Forall_inv_tail HFF).
Qed.

Lemma sub_0_lt_ymx : ∀ x y,
  0 <= x → x < y → 0 < y - x.
Proof.
  intros x y Hle Hlt.
  destruct x as [|a].
  - rewrite Nat.sub_0_r.
    exact Hlt.
  - rewrite <- Nat.lt_add_lt_sub_l.
    rewrite Nat.add_0_r.
    exact Hlt.
Qed.

Lemma mod_sub : ∀ x m,
  0 < m → 0 < m - (x mod m) <= m.
Proof.
  intros x m Hlt.
  constructor.
  - assert (0 <= x mod m < m) as HmRange. {
      apply Nat.mod_bound_pos.
      apply Nat.le_0_l.
      exact Hlt.
    }
    destruct HmRange as [HA HB].
    remember (x mod m) as y.
    apply (sub_0_lt_ymx y m HA HB).
  - assert (x mod m < m) as HmRange. {
      apply Nat.mod_upper_bound.
      apply Nat.neq_sym.
      apply Nat.lt_neq.
      exact Hlt.
    }
    apply Nat.le_sub_l.
Qed.

Lemma mod_opposition : ∀ x a,
  0 ≠ a → x mod a + (a - x mod a) = a.
Proof.
  intros x a Hnz.
  assert (x mod a < a) as Hxma. {
    apply (Nat.mod_upper_bound).
    apply Nat.neq_sym.
    exact Hnz.
  }
  remember (x mod a) as y eqn:Heqy.
  apply Minus.le_plus_minus_r.
  apply (Nat.lt_le_incl _ _ Hxma).
Qed.

Theorem binaryEvalPaddedBytesAligned : ∀ bs a (Hnz : 0 ≠ a),
  length (binaryEvalPaddedBytes bs a Hnz) mod a = 0.
Proof.
  intros bs a Hnz.
  unfold binaryEvalPaddedBytes.
  destruct (Datatypes.length bs mod a) eqn:Hlen.
  - rewrite map_length.
    exact Hlen.
  - rewrite map_length.
    rewrite app_length.
    rewrite repeat_length.
    rewrite <- Hlen.
    remember (Datatypes.length bs) as x.
    rewrite <- (Nat.add_mod_idemp_l x (a - x mod a) a).
    assert ((x mod a + (a - x mod a)) = a) as Heqa. {
      rewrite (mod_opposition x a Hnz).
      reflexivity.
    }
    rewrite Heqa.
    apply Nat.mod_same.
    apply Nat.neq_sym; exact Hnz.
    apply Nat.neq_sym; exact Hnz.
Qed.

Lemma repeat_eq : ∀ (A : Type) (P : A → Prop) (n : nat) (x : A),
  Forall (eq x) (repeat x n).
Proof.
  intros A P n x.
  induction n as [|m Hm].
  - constructor.
  - simpl.
    constructor.
    reflexivity.
    exact Hm.
Qed.

Lemma Forall_implies : ∀ (A : Type) (P : A → Prop) (Q : A → Prop) (xs : list A) (H : ∀ x, P x → Q x),
  Forall P xs → Forall Q xs.
Proof.
  intros A P Q xs Ht HforAll.
  induction HforAll as [|y ys Hpy HfaP HfaQ].
  - constructor.
  - constructor.
    apply (Ht y Hpy).
    exact HfaQ.
Qed.

Theorem binaryEvalPaddedBytesU8 : ∀ bs a (Hnz : 0 ≠ a),
  Forall streamEIsU8 (binaryEvalPaddedBytes bs a Hnz).
Proof.
  intros bs a Hnz.
  unfold binaryEvalPaddedBytes.
  destruct (Datatypes.length bs mod a) as [|HB].
  - rewrite Forall_map.
    induction bs as [|r rs Hrs].
    -- constructor.
    -- constructor.
       reflexivity.
       exact Hrs.
  - rewrite map_app.
    assert (Forall streamEIsU8 (map u8byte bs)) as Hmap. {
      rewrite Forall_map.
      induction bs as [|r rs Hrs].
      - constructor.
      - constructor.
        reflexivity.
        exact Hrs.
    }
    assert (Forall streamEIsU8 (map u8byte (repeat "000"%byte (a - S HB)))) as HmapR. {
      rewrite Forall_map.
      assert (Forall (eq "000"%byte) (repeat "000"%byte (a - S HB))) as Hfeq
        by (apply (repeat_eq byte (λ _ : byte, True) (a - S HB) "000"%byte)).
      simpl.
      apply (@Forall_implies byte (eq "000"%byte) (λ _ : byte, True) (repeat "000"%byte (a - S HB))). {
        intros. exact I.
      }
      exact Hfeq.
    }
    apply Forall_app.
    constructor.
    exact Hmap.
    exact HmapR.
Qed.

Lemma app_cons : ∀ (A : Type) (x : A) (xs : list A),
  x :: xs = app (cons x nil) xs.
Proof.
  intros A x xs.
  reflexivity.
Qed.

Theorem binaryEvalStreamsWellFormed : ∀ b,
  streamWellFormed (binaryEval b).
Proof.
  intros b.
  induction b as [a0|a1|a2|a3|a4 Hfa|a5|a6 Hfa].
  (* U32 *)
  - apply BEPVu32.
  (* U64 *)
  - apply BEPVu64.
  (* Bytes *)
  - unfold binaryEval.
    rewrite app_cons.
    apply BEPAppend.
    apply BEPVu32.
    assert (length (binaryEvalPaddedBytes a2 4 p0not4) mod 4 = 0) as Hlm
      by (apply (binaryEvalPaddedBytesAligned)).
    apply BEPVu8s.
    apply binaryEvalPaddedBytesU8.
    exact Hlm.
  (* UTF-8 *)
  - unfold binaryEval.
    rewrite app_cons.
    apply BEPAppend.
    apply BEPVu32.
    assert (length (binaryEvalPaddedBytes a3 4 p0not4) mod 4 = 0) as Hlm
      by (apply (binaryEvalPaddedBytesAligned)).
    assert (Forall streamEIsU8 (binaryEvalPaddedBytes a3 4 p0not4)) as Hu8
      by (apply (binaryEvalPaddedBytesU8)).
    apply (BEPVu8s _ Hu8 Hlm).
  (* Array *)
  - simpl.
    rewrite app_cons.
    apply BEPAppend.
    apply BEPVu32.
    induction a4 as [|q qs IHqs].
    -- constructor.
    -- assert (streamWellFormed (concat (map binaryEval qs))) as HqsWF
         by (apply (IHqs (Forall_inv_tail Hfa))).
       assert (streamWellFormed (binaryEval q)) as HqWF
         by (apply (Forall_inv Hfa)).
       simpl.
       apply BEPAppend.
       exact HqWF.
       exact HqsWF.
  (* Reserve *)
  - simpl.
    unfold asMultipleOf4.
    remember (asMultipleOf a5 4 p0not4) as size eqn:Heqsize.
    assert (size mod 4 = 0) as Heqm. {
      rewrite Heqsize.
      apply (asMultipleOfMod).
    }
    assert ((Vu8 ∘ Byte.to_nat) "000"%byte = (Vu8 0)) as HbyteEq by reflexivity.
    apply BEPVu8s.
    assert (Forall (eq (Vu8 0)) (repeat (Vu8 0) size)) as Hfeq
      by (apply (@repeat_eq streamE streamEIsU8 size (Vu8 0))).
    apply (@Forall_implies streamE (eq (Vu8 0)) streamEIsU8 (repeat (Vu8 0) size)). {
      intros x Hxeq.
      unfold streamEIsU8.
      rewrite <- Hxeq.
      exact I.
    }
    exact Hfeq.
    rewrite repeat_length.
    exact Heqm.
  (* Record *)
  - simpl.
    induction a6 as [|q qs IHqs].
    -- constructor.
    -- assert (Forall (λ b : binaryExp, streamWellFormed (binaryEval b)) (map snd qs)) as Hfqs. {
         apply (@Forall_inv_tail binaryExp (λ b : binaryExp, streamWellFormed (binaryEval b)) (snd q) (map snd qs)). {
           assert ((map snd (q :: qs)) = (snd q :: map snd qs)) as Hmc by reflexivity.
           rewrite <- Hmc.
           exact Hfa.
         }
       }
       assert (streamWellFormed (concat (map (binaryEval ∘ snd) qs))) as Hconqs by (apply (IHqs Hfqs)).
       rewrite map_cons.
       rewrite concat_cons.
       apply BEPAppend.
       rewrite map_cons in Hfa.
       apply (Forall_inv Hfa).
       exact Hconqs.
Qed.

Unset Mangle Names.

Lemma fold_right_1_length : ∀ xs,
  Forall (eq 1) xs → fold_right add 0 xs = length xs.
Proof.
  intros xs Hfa.
  induction xs as [|y ys IHxs].
  - reflexivity.
  - rewrite <- fold_right_add_cons.
    assert (length (y :: ys) = 1 + length (ys)) as HlenYs by reflexivity.
    rewrite HlenYs.
    assert (1 = y) as Hy1 by (apply (Forall_inv Hfa)).
    rewrite <- Hy1.
    f_equal.
    apply IHxs.
    apply (Forall_inv_tail Hfa).
Qed.

Theorem fold_right_add_app : ∀ xs ys,
  fold_right add 0 xs + fold_right add 0 ys = fold_right add 0 (xs ++ ys).
Proof.
  intros xs ys.
  rewrite fold_right_app.
  generalize dependent ys.
  induction xs as [|q qs IHqs].
  - reflexivity.
  - intros ys.
    simpl.
    rewrite <- (IHqs ys).
    rewrite Nat.add_assoc.
    reflexivity.
Qed.

Theorem streamSizeApp : ∀ xs ys,
  streamSize xs + streamSize ys = streamSize (xs ++ ys).
Proof.
  intros xs ys.
  unfold streamSize.
  rewrite map_app.
  rewrite fold_right_add_app.
  reflexivity.
Qed.

Theorem streamsWellFormedDivisible4 : ∀ es,
  streamWellFormed es → streamSize es mod 4 = 0.
Proof.
  intros es Hwf.
  induction Hwf as [|H1|H2|es Hfa Hsize|xs ys Hxswf Hxsize Hyswf Hysize].
  - reflexivity.
  - reflexivity.
  - reflexivity.
  - unfold streamSize.
    assert (Forall (λ e, 1 = streamElementSize e) es) as HFaSize. {
      apply (@Forall_implies streamE streamEIsU8 (λ e : streamE, 1 = streamElementSize e) es). {
        intros x His.
        destruct x as [u64|u32|u8].
        - contradiction.
        - contradiction.
        - reflexivity.
      }
      exact Hfa.
    }
    assert (Forall (eq 1) (map streamElementSize es)) as Hall1. {
      apply (@Forall_map _ _ _ _ es).
      exact HFaSize.
    }
    assert (fold_right add 0 (map streamElementSize es) = length es) as HlenEq. {
      assert (length es = length (map streamElementSize es)) as HmapLen. {
        rewrite map_length.
        reflexivity.
      }
      rewrite HmapLen.
      apply (fold_right_1_length (map streamElementSize es) Hall1).
    }
    rewrite HlenEq.
    exact Hsize.
  - rewrite <- streamSizeApp.
    apply divisiblityNAdd.
    discriminate.
    exact Hxsize.
    exact Hysize.
Qed.

5.5. Calino/ByteOrder.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Lists.List.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Divisible8.
Require Import Calino.Descriptor.

Import ListNotations.

Inductive byteOrder : Set :=
  | ByteOrderBig
  | ByteOrderLittle.

Inductive bit : Set :=
  | B0
  | B1.

Inductive octet : Set :=
  | OctExact  : bit → bit → bit → bit → bit → bit → bit → bit → octet
  | OctRemain : bit → bit → bit → bit → bit → bit → bit → bit → octet.

Definition octetIsRemainder (o : octet): Prop :=
  match o with
  | OctExact  _ _ _ _ _ _ _ _ => False
  | OctRemain _ _ _ _ _ _ _ _ => True
  end.

Definition octetIsExact (o : octet): Prop :=
  match o with
  | OctExact  _ _ _ _ _ _ _ _ => True
  | OctRemain _ _ _ _ _ _ _ _ => False
  end.

Lemma octetIsRemainderNotExact : ∀ (o : octet), octetIsRemainder o → ¬octetIsExact o.
Proof.
  intros o Hrem Hfalse.
  destruct o; contradiction.
Qed.

Lemma octetIsExactNotRemainder : ∀ (o : octet), octetIsExact o → ¬octetIsRemainder o.
Proof.
  intros o Hrem Hfalse.
  destruct o; contradiction.
Qed.

Inductive bitsOctetsHasRemainder : list octet → Prop :=
  | BOHasRemainder : ∀ (prefix : list octet) (o : octet),
    Forall octetIsExact prefix →
      octetIsRemainder o →
        bitsOctetsHasRemainder (prefix ++ o :: []).

Fixpoint octetsBigEndianAux
  (bits   : list bit)
  (octets : list octet)
: list octet :=
  match bits with
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: rest) =>
    octets ++ [OctExact b7 b6 b5 b4 b3 b2 b1 b0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 b2 b1 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 b2 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: b3 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 b3 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: b4 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 b4 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: b5 :: rest) =>
    octets ++ [OctRemain b7 b6 b5 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: b6 :: rest) =>
    octets ++ [OctRemain b7 b6 B0 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | (b7 :: rest) =>
    octets ++ [OctRemain b7 B0 B0 B0 B0 B0 B0 B0] ++ octetsBigEndianAux rest []
  | [] =>
    octets
  end.

Definition octetsBigEndian (bits : list bit) : list octet :=
  octetsBigEndianAux bits [].

Definition octetsLittleEndian (bits : list bit) : list octet :=
  rev (octetsBigEndianAux bits []).

Definition listInduction8 :
  ∀ (A : Type),
  ∀ (P : list A → Prop),
  P [] →
  (∀ (b0                      : A), P (b0 :: [])) →
  (∀ (b1 b0                   : A), P (b1 :: b0 :: [])) →
  (∀ (b2 b1 b0                : A), P (b2 :: b1 :: b0 :: [])) →
  (∀ (b3 b2 b1 b0             : A), P (b3 :: b2 :: b1 :: b0 :: [])) →
  (∀ (b4 b3 b2 b1 b0          : A), P (b4 :: b3 :: b2 :: b1 :: b0 :: [])) →
  (∀ (b5 b4 b3 b2 b1 b0       : A), P (b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: [])) →
  (∀ (b6 b5 b4 b3 b2 b1 b0    : A), P (b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: [])) →
  (∀ (b7 b6 b5 b4 b3 b2 b1 b0 : A) (rest : list A), P rest → P (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: rest)) →
  ∀ (L : list A), P L :=
  λ A P P0 P1 P2 P3 P4 P5 P6 P7 P8,
  fix f (l : list A) :=
    match l with
    | []                                                     => P0
    | x0 :: []                                               => P1 x0
    | (x0 :: x1 :: [])                                       => P2 x0 x1
    | (x0 :: x1 :: x2 :: [])                                 => P3 x0 x1 x2
    | (x0 :: x1 :: x2 :: x3 :: [])                           => P4 x0 x1 x2 x3
    | (x0 :: x1 :: x2 :: x3 :: x4 :: [])                     => P5 x0 x1 x2 x3 x4
    | (x0 :: x1 :: x2 :: x3 :: x4 :: x5 :: [])               => P6 x0 x1 x2 x3 x4 x5
    | (x0 :: x1 :: x2 :: x3 :: x4 :: x5 :: x6 :: [])         => P7 x0 x1 x2 x3 x4 x5 x6
    | (x0 :: x1 :: x2 :: x3 :: x4 :: x5 :: x6 :: x7 :: rest) => P8 x0 x1 x2 x3 x4 x5 x6 x7 rest (f rest)
    end.

Lemma app_non_empty : ∀ (A : Type) (xs : list A) (y : A),
  xs ++ [y] ≠ [].
Proof.
  intros A xs y.
  unfold not.
  destruct xs as [|z zs].
    intros Hfalse; inversion Hfalse.
    intros Hfalse; inversion Hfalse.
Qed.

Lemma app_list_implies_eq : ∀ (A : Type) (x y : A) (xs : list A),
  xs ++ [x] = [y] → xs = [] ∧ x = y.
Proof.
  intros A x y xs Happ.
  induction xs as [|z zs] eqn:Hxe.
  - constructor. reflexivity.
    rewrite (app_nil_l [x]) in Happ.
    injection Happ as Heq; exact Heq.
  - inversion Happ.
    assert (zs ++ [x] ≠ []) by (apply app_non_empty).
    contradiction.
Qed.

Lemma p8notZ : 8 ≠ 0.
Proof. discriminate. Qed.

Lemma list_mod8_0 : ∀ (A : Type) (xs : list A) (n7 n6 n5 n4 n3 n2 n1 n0 : A),
  divisible8 (length xs) → divisible8 (length (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: xs)).
Proof.
  intros A xs n7 n6 n5 n4 n3 n2 n1 n0 Hlen8.
  unfold divisible8 in *.
  assert (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: xs
       = (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: []) ++ xs) as HlistEq
          by reflexivity.
  rewrite HlistEq.
  rewrite app_length.
  assert (length [n7; n6; n5; n4; n3; n2; n1; n0] = 8) as Hprefix8 by reflexivity.
  rewrite Hprefix8.
  rewrite <- (Nat.add_mod_idemp_l 8 (length xs) 8 p8notZ).
  rewrite (Nat.mod_same 8 p8notZ).
  rewrite (Nat.add_0_l).
  exact Hlen8.
Qed.

Lemma list_mod8_1 : ∀ (A : Type) (xs : list A) (n7 n6 n5 n4 n3 n2 n1 n0 : A),
  divisible8 (length (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: xs)) → divisible8 (length xs).
Proof.
  intros A xs n7 n6 n5 n4 n3 n2 n1 n0 Hlen8.
  unfold divisible8 in *.
  assert (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: xs
       = (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: []) ++ xs) as HlistEq
          by reflexivity.
  rewrite HlistEq in Hlen8.
  rewrite app_length in Hlen8.
  assert (length [n7; n6; n5; n4; n3; n2; n1; n0] = 8) as Hprefix8 by reflexivity.
  rewrite Hprefix8 in Hlen8.
  rewrite <- (Nat.add_mod_idemp_l 8 (length xs) 8 p8notZ) in Hlen8.
  rewrite (Nat.mod_same 8 p8notZ) in Hlen8.
  rewrite (Nat.add_0_l) in Hlen8.
  exact Hlen8.
Qed.

Theorem list_mod8 : ∀ (A : Type) (xs : list A) (n7 n6 n5 n4 n3 n2 n1 n0 : A),
  divisible8 (length xs) ↔ divisible8 (length (n7 :: n6 :: n5 :: n4 :: n3 :: n2 :: n1 :: n0 :: xs)).
Proof.
  intros A xs n7 n6 n5 n4 n3 n2 n1 n0.
  constructor.
  - apply list_mod8_0.
  - apply list_mod8_1.
Qed.

Theorem octetsBigEndianLengthDivisibleAllExact : ∀ (b : list bit),
  divisible8 (length b) → Forall octetIsExact (octetsBigEndian b).
Proof.
  intros b Hlen8.
  unfold octetsBigEndian.
  induction b using listInduction8.
  - constructor.
  - inversion Hlen8.
  - inversion Hlen8.
  - inversion Hlen8.
  - inversion Hlen8.
  - inversion Hlen8.
  - inversion Hlen8.
  - inversion Hlen8.
  - simpl.
    rewrite <- list_mod8 in Hlen8.
    assert (Forall octetIsExact (octetsBigEndianAux b []))   as HallExact by (apply (IHb Hlen8)).
    assert (octetIsExact (OctExact b7 b6 b5 b4 b3 b2 b1 b0)) as Hexact    by constructor.
    apply (@Forall_cons octet octetIsExact (OctExact b7 b6 b5 b4 b3 b2 b1 b0) (octetsBigEndianAux b []) Hexact HallExact).
Qed.

Theorem octetsLittleEndianLengthDivisibleAllExact : ∀ (b : list bit),
  divisible8 (length b) → Forall octetIsExact (octetsLittleEndian b).
Proof.
  intros b Hlen8.
  apply (Forall_rev (octetsBigEndianLengthDivisibleAllExact b Hlen8)).
Qed.

Theorem octetsBigEndianLengthDivisibleNoRemainder : ∀ (b : list bit),
  Forall octetIsExact (octetsBigEndian b) → ¬ bitsOctetsHasRemainder (octetsBigEndian b).
Proof.
  intros b HallExact.
  unfold octetsBigEndian.
  intro Hfalse.
  inversion Hfalse as [prefix o HprefixAllExact HoIsRemainder HprefixEq].
  unfold octetsBigEndian in HallExact.
  (* We know that everything in the list is exact. *)
  (* We can show that o must be in this list according to HprefixEq. *)
  assert (In o (octetsBigEndianAux b [])) as HoInB. {
    assert (In o (prefix ++ [o])) as HoInPrefix by (apply (in_elt o prefix [])).
    rewrite HprefixEq in HoInPrefix.
    exact HoInPrefix.
  }
  (* And because o is in the list, it must be exact. *)
  assert (octetIsExact o) as HoIsExact. {
    rewrite Forall_forall in HallExact.
    apply (HallExact o HoInB).
  }
  (* There is a contradiction; o cannot be both exact and a remainder. *)
  apply (octetIsExactNotRemainder o HoIsExact HoIsRemainder).
Qed.

Lemma mod_8_lt_0 : ∀ (m : nat),
  0 < m mod 8 → 0 < (m + 8) mod 8.
Proof.
  intros m Hlt.
  rewrite (Nat.add_mod m 8 8).
  rewrite (Nat.mod_same).
  rewrite (Nat.add_0_r).
  rewrite (Nat.mod_mod).
  exact Hlt.
  discriminate.
  discriminate.
  discriminate.
Qed.

Lemma mod_8_lt_1 : ∀ (m : nat),
  0 < (m + 8) mod 8 -> 0 < m mod 8.
Proof.
  intros m Hlt.
  rewrite (Nat.add_mod m 8 8) in Hlt.
  rewrite (Nat.mod_same)      in Hlt.
  rewrite (Nat.add_0_r)       in Hlt.
  rewrite (Nat.mod_mod)       in Hlt.
  exact Hlt.
  discriminate.
  discriminate.
  discriminate.
Qed.

Lemma mod_8_lt : ∀ (m : nat),
  0 < (m + 8) mod 8 ↔ 0 < m mod 8.
Proof.
  constructor.
  apply mod_8_lt_1.
  apply mod_8_lt_0.
Qed.

Theorem octetsBigEndianLengthIndivisibleRemainder : ∀ (b : list bit),
  0 < length b mod 8 → ∃ o, In o (octetsBigEndian b) ∧ octetIsRemainder o.
Proof.
  intros b Hlength.
  induction b using listInduction8.
  - inversion Hlength.
  - exists (OctRemain b0 B0 B0 B0 B0 B0 B0 B0).
    constructor.
    left. reflexivity.
    constructor.
  - exists (OctRemain b1 b0 B0 B0 B0 B0 B0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - exists (OctRemain b2 b1 b0 B0 B0 B0 B0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - exists (OctRemain b3 b2 b1 b0 B0 B0 B0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - exists (OctRemain b4 b3 b2 b1 b0 B0 B0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - exists (OctRemain b5 b4 b3 b2 b1 b0 B0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - exists (OctRemain b6 b5 b4 b3 b2 b1 b0 B0).
    constructor.
    left.
    constructor.
    constructor.
  - assert (0 < length b mod 8) as Hlt. {
      assert (length (b7 :: b6 :: b5 :: b4 :: b3 :: b2 :: b1 :: b0 :: b) = length b + 8) as Heq
        by (rewrite Nat.add_comm; reflexivity).
      rewrite Heq in Hlength.
      rewrite <- (mod_8_lt (length b)).
      exact Hlength.
    }
    assert (∃ o : octet, In o (octetsBigEndian b) ∧ octetIsRemainder o) as HEx
      by (apply (IHb Hlt)).
    destruct HEx as [ox [HoxIn HoxRem]].
    simpl.
    exists ox.
    constructor.
    right.
    exact HoxIn.
    exact HoxRem.
Qed.

Theorem octetsLittleEndianLengthIndivisibleRemainder : ∀ (b : list bit),
  0 < length b mod 8 → ∃ o, In o (octetsLittleEndian b) ∧ octetIsRemainder o.
Proof.
  unfold octetsLittleEndian.
  intros b Hlen.
  assert (∃ o, In o (octetsBigEndian b) ∧ octetIsRemainder o) as Hexists
    by (apply (octetsBigEndianLengthIndivisibleRemainder b Hlen)).
  destruct Hexists as [ox [HoxIn HoxRem]].
  exists ox.
  rewrite <- (in_rev (octetsBigEndianAux b [])).
  constructor.
  exact HoxIn.
  exact HoxRem.
Qed.

Require Import Coq.Strings.String.

Definition byteOrderDescribe (b : byteOrder) : descriptor :=
  match b with
  | ByteOrderBig    => "BIG_ENDIAN"
  | ByteOrderLittle => "LITTLE_ENDIAN"
  end.

#[export]
Instance byteOrderDescribable : describable byteOrder := {
  descriptorOf f := byteOrderDescribe f
}.

5.6. Calino/ChannelDescription.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Strings.String.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.ChannelSemantic.
Require Import Calino.Descriptor.
Require Import Calino.StringUtility.
Require Import Calino.Divisible8.

Import ListNotations.

Set Mangle Names.

Inductive channelDescription : Set := channelDescriptionMake {
  cdSemantic    : channelSemantic;
  cdBits        : nat;
  cdBitsNonzero : 0 ≠ cdBits
}.

Definition channelDescriptionDescribe (c : channelDescription) : descriptor :=
  descriptorOf (cdSemantic c) ++ stringOfNat (cdBits c).

#[export]
Instance channelDescriptionDescribable : describable channelDescription := {
  descriptorOf c := channelDescriptionDescribe c
}.

Fixpoint channelDescriptionsDescribe (c : list channelDescription) : descriptor :=
  match c with
  | nil        => ""
  | cons d nil => channelDescriptionDescribe d
  | cons d e   => (channelDescriptionDescribe d) ++ ":" ++ (channelDescriptionsDescribe e)
  end.

Inductive channelLayoutPacking : Set :=
  | CLPack8
  | CLPack16
  | CLPack32
  | CLPack64.

Definition channelLayoutPackingBits (c : channelLayoutPacking) : nat :=
  match c with
  | CLPack8  => 8
  | CLPack16 => 16
  | CLPack32 => 32
  | CLPack64 => 64
  end.

Theorem channelLayoutPackingBitsDiv8 : ∀ c, divisible8 (channelLayoutPackingBits (c)).
Proof.
  intros c.
  destruct c; reflexivity.
Qed.

Definition channelLayoutPackingDescribe (c : channelLayoutPacking) : descriptor :=
  match c with
  | CLPack8  => "p8"
  | CLPack16 => "p16"
  | CLPack32 => "p32"
  | CLPack64 => "p64"
  end.

#[export]
Instance channelLayoutPackingDescribable : describable channelLayoutPacking := {
  descriptorOf c := channelLayoutPackingDescribe c
}.

Definition channelDescriptionBitsDivisible8 (c : channelDescription) : Prop :=
  divisible8 (cdBits c).

Fixpoint channelDescriptionsBitsTotal (c : list channelDescription) : nat :=
  match c with
  | nil         => 0
  | (x :: rest) => (cdBits x) + (channelDescriptionsBitsTotal rest)
  end.

Lemma natAddNonzero : ∀ (n m : nat), 0 ≠ n → 0 ≠ m + n.
Proof.
  intros n m HnZ.
  destruct m; simpl; auto.
Qed.

Lemma channelDescriptionsBitsNonEmptyNonZero : ∀ (c : list channelDescription),
  nil ≠ c → 0 ≠ channelDescriptionsBitsTotal c.
Proof.
  intros c HnotNil.
  induction c as [|a b]. {
    contradiction.
  } {
    simpl.
    assert (0 ≠ cdBits a) as HbitsNZ
      by apply (cdBitsNonzero a).
    assert (0 ≠ channelDescriptionsBitsTotal b + cdBits a) as Hnz2. {
      apply natAddNonzero.
      exact HbitsNZ.
    }
    rewrite (Nat.add_comm) in Hnz2.
    exact Hnz2.
  }
Qed.

Inductive channelLayoutDescriptionUnpacked : Set := CLDUMake {
  uChannels         : list channelDescription;
  uChannelsNonEmpty : [] ≠ uChannels;
  uInvariants       : Forall channelDescriptionBitsDivisible8 uChannels;
}.

Definition channelLayoutDescriptionUnpackedDescribe (c : channelLayoutDescriptionUnpacked) : descriptor :=
  channelDescriptionsDescribe (uChannels c).

#[export]
Instance channelLayoutDescriptionUnpackedDescribable : describable channelLayoutDescriptionUnpacked := {
  descriptorOf c := channelLayoutDescriptionUnpackedDescribe c
}.

Inductive channelLayoutDescriptionPacked : Set := CLDPMake {
  pChannels         : list channelDescription;
  pChannelsNonEmpty : [] ≠ pChannels;
  pPacking          : channelLayoutPacking;
  pInvariants       : channelDescriptionsBitsTotal pChannels = channelLayoutPackingBits pPacking
}.

Definition channelLayoutDescriptionPackedDescribe (c : channelLayoutDescriptionPacked) : descriptor :=
  let packing := descriptorOf (pPacking c) in
  let channels := channelDescriptionsDescribe (pChannels c) in
    packing ++ "|" ++ channels.

#[export]
Instance channelLayoutDescriptionPackedDescribable : describable channelLayoutDescriptionPacked := {
  descriptorOf c := channelLayoutDescriptionPackedDescribe c
}.

Inductive channelLayoutDescription : Set :=
  | ChannelLayoutDescriptionUnpacked : channelLayoutDescriptionUnpacked → channelLayoutDescription
  | ChannelLayoutDescriptionPacked   : channelLayoutDescriptionPacked   → channelLayoutDescription.

Definition channelLayoutDescriptionDescribe (c : channelLayoutDescription) : descriptor :=
  match c with
  | ChannelLayoutDescriptionPacked p   => descriptorOf p
  | ChannelLayoutDescriptionUnpacked u => descriptorOf u
  end.

#[export]
Instance channelLayoutDescriptionDescribable : describable channelLayoutDescription := {
  descriptorOf c := channelLayoutDescriptionDescribe c
}.

Definition channelLayoutDescriptionBits (c : channelLayoutDescription) : nat :=
  match c with
  | ChannelLayoutDescriptionUnpacked u =>
    channelDescriptionsBitsTotal (uChannels u)
  | ChannelLayoutDescriptionPacked p =>
    channelDescriptionsBitsTotal (pChannels p)
  end.

Lemma channelLayoutDescriptionBitsAdd : ∀ d ds,
  channelDescriptionsBitsTotal (d :: ds) =
    (cdBits d) + (channelDescriptionsBitsTotal ds).
Proof. intros d ds. reflexivity. Qed.

Theorem channelLayoutDescriptionBitsDivisible8 : ∀ (c : channelLayoutDescription),
  divisible8 (channelLayoutDescriptionBits c).
Proof.
  intros c.
  destruct c as [u|p]. {
    assert (Forall channelDescriptionBitsDivisible8 (uChannels u)) as Hf8
      by (apply uInvariants).
    unfold channelLayoutDescriptionBits.
    induction (uChannels u) as [|d ds IHu]. {
      reflexivity.
    } {
      rewrite channelLayoutDescriptionBitsAdd.
      assert (divisible8 (channelDescriptionsBitsTotal ds)) as Hdsdiv8. {
        assert (Forall channelDescriptionBitsDivisible8 ds) as Hfac
          by (apply (Forall_inv_tail (a := d) (l := ds) Hf8)).
        apply (IHu Hfac).
      }
      assert (divisible8 (cdBits d)) as Hdivbits
        by (apply (Forall_inv (a := d) (l := ds) Hf8)).
      apply (divisiblity8Add (cdBits d) (channelDescriptionsBitsTotal ds) Hdivbits Hdsdiv8).
    }
  } {
    simpl.
    assert (channelDescriptionsBitsTotal (pChannels p) = channelLayoutPackingBits (pPacking p))
      as Hbeq by (apply pInvariants).
    rewrite Hbeq.
    apply channelLayoutPackingBitsDiv8.
  }
Qed.

Theorem channelLayoutDescriptionBitsLe8 : ∀ (c : channelLayoutDescription),
  8 <= channelLayoutDescriptionBits c.
Proof.
  intros c.
  assert (divisible8 (channelLayoutDescriptionBits c)) as Hdiv8
    by (apply (channelLayoutDescriptionBitsDivisible8 c)).
  unfold divisible8 in Hdiv8.

  destruct c as [u|p].
  - simpl.
    destruct (uChannels u) as [|ch0 chs] eqn:Hcheq.
    -- symmetry in Hcheq.
       assert ([] ≠ uChannels u) as Hne by (apply (uChannelsNonEmpty u)).
       contradiction.
    -- unfold channelLayoutDescriptionBits in Hdiv8.
       rewrite Nat.mod_divide in Hdiv8.
       rewrite <- Hcheq.
       apply (Nat.divide_pos_le 8 (channelDescriptionsBitsTotal (uChannels u))).
       rewrite Hcheq.
       simpl.
       assert (0 < cdBits ch0) as HbitnZ. {
         apply Lt.neq_0_lt.
         apply (cdBitsNonzero ch0).
       }
       apply Nat.add_pos_l.
       exact HbitnZ.
       exact Hdiv8.
       discriminate.
  - simpl.
    rewrite (pInvariants p).
    destruct (pPacking p) eqn:Hpack.
    -- constructor.
    -- repeat (constructor).
    -- repeat (constructor).
    -- repeat (constructor).
Qed.

5.7. Calino/ChannelSemantic.v

Require Import Coq.Strings.String.

Require Import Calino.Descriptor.

Inductive channelSemantic : Set :=
  | CSRed
  | CSGreen
  | CSBlue
  | CSAlpha
  | CSDepth
  | CSStencil
  | CSExponent
  | CSUnused.

Definition channelSemanticDescribe (c : channelSemantic) : descriptor :=
  match c with
  | CSRed      => "R"
  | CSGreen    => "G"
  | CSBlue     => "B"
  | CSAlpha    => "A"
  | CSDepth    => "D"
  | CSStencil  => "S"
  | CSExponent => "E"
  | CSUnused   => "X"
  end.

#[export]
Instance channelSemanticDescribable : describable channelSemantic := {
  descriptorOf c := channelSemanticDescribe c
}.

5.8. Calino/ChannelType.v

Require Import Coq.Strings.String.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Inductive channelType : Set :=
  | CTFixedPointNormalizedUnsigned
  | CTFixedPointNormalizedSigned
  | CTScaledUnsigned
  | CTScaledSigned
  | CTIntegerUnsigned
  | CTIntegerSigned
  | CTFloatIEEE754
  | CTCustom : descriptor → channelType.

Definition channelTypeDescribe (c : channelType) : descriptor :=
  match c with
  | CTFixedPointNormalizedUnsigned => "FIXED_POINT_NORMALIZED_UNSIGNED"
  | CTFixedPointNormalizedSigned   => "FIXED_POINT_NORMALIZED_SIGNED"
  | CTScaledUnsigned               => "SCALED_UNSIGNED"
  | CTScaledSigned                 => "SCALED_SIGNED"
  | CTIntegerUnsigned              => "INTEGER_UNSIGNED"
  | CTIntegerSigned                => "INTEGER_SIGNED"
  | CTFloatIEEE754                 => "FLOATING_POINT_IEEE754"
  | CTCustom d                     => d
  end.

#[export]
Instance channelTypeDescribable : describable channelType := {
  descriptorOf c := channelTypeDescribe c
}.

5.9. Calino/ColorSpace.v

Require Import Coq.Strings.String.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Inductive colorSpace : Set :=
  | CSLinear
  | CSsRGB
  | CSCustom : descriptor → colorSpace.

Definition colorSpaceDescribe (c : colorSpace) : descriptor :=
  match c with
  | CSLinear   => "LINEAR"
  | CSsRGB     => "SRGB"
  | CSCustom d => d
  end.

#[export]
Instance colorSpaceDescribable : describable colorSpace := {
  descriptorOf c := colorSpaceDescribe c
}.

5.10. Calino/Compression.v

Require Import Coq.Strings.String.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Inductive compressionMethod : Set :=
  | CompressionUncompressed
  | CompressionBC1
  | CompressionBC2
  | CompressionBC3
  | CompressionBC4
  | CompressionBC5
  | CompressionBC6
  | CompressionBC7
  | CompressionETC1
  | CompressionETC2
  | CompressionEAC
  | CompressionASTC : nat → nat → compressionMethod
  | CompressionCustom :
    ∀ (d : descriptor)
      (blockSizeX : nat)
      (blockSizeY : nat)
      (identifier : nat)
      (align : nat), 0 < align → compressionMethod.

Definition compressionMethodDescriptor (c : compressionMethod) :=
  match c with
  | CompressionUncompressed       => "UNCOMPRESSED"
  | CompressionBC1                => "BC1"
  | CompressionBC2                => "BC2"
  | CompressionBC3                => "BC3"
  | CompressionBC4                => "BC4"
  | CompressionBC5                => "BC5"
  | CompressionBC6                => "BC6"
  | CompressionBC7                => "BC7"
  | CompressionETC1               => "ETC1"
  | CompressionETC2               => "ETC2"
  | CompressionEAC                => "EAC"
  | CompressionASTC _ _           => "ASTC"
  | CompressionCustom c _ _ _ _ _ => c
  end.

Definition compressionBlockSizeX (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 4
  | CompressionBC2                => 4
  | CompressionBC3                => 4
  | CompressionBC4                => 4
  | CompressionBC5                => 4
  | CompressionBC6                => 4
  | CompressionBC7                => 4
  | CompressionETC1               => 4
  | CompressionETC2               => 4
  | CompressionEAC                => 4
  | CompressionASTC x _           => x
  | CompressionCustom _ x _ _ _ _ => x
  end.

Definition compressionBlockSizeY (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 4
  | CompressionBC2                => 4
  | CompressionBC3                => 4
  | CompressionBC4                => 4
  | CompressionBC5                => 4
  | CompressionBC6                => 4
  | CompressionBC7                => 4
  | CompressionETC1               => 4
  | CompressionETC2               => 4
  | CompressionEAC                => 4
  | CompressionASTC _ y           => y
  | CompressionCustom _ _ y _ _ _ => y
  end.

Definition compressionSectionIdentifier (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 0
  | CompressionBC2                => 0
  | CompressionBC3                => 0
  | CompressionBC4                => 0
  | CompressionBC5                => 0
  | CompressionBC6                => 0
  | CompressionBC7                => 0
  | CompressionETC1               => 0
  | CompressionETC2               => 0
  | CompressionEAC                => 0
  | CompressionASTC _ _           => 0
  | CompressionCustom _ _ _ i _ _ => i
  end.

Definition compressionBlockAlignment (c : compressionMethod) : nat :=
  match c with
  | CompressionUncompressed       => 0
  | CompressionBC1                => 8
  | CompressionBC2                => 16
  | CompressionBC3                => 16
  | CompressionBC4                => 8
  | CompressionBC5                => 16
  | CompressionBC6                => 16
  | CompressionBC7                => 16
  | CompressionETC1               => 16
  | CompressionETC2               => 16
  | CompressionEAC                => 16
  | CompressionASTC _ _           => 16
  | CompressionCustom _ _ _ _ a _ => a
  end.

Definition compressionIsNotCompressed (c : compressionMethod) : Prop :=
  match c with
  | CompressionUncompressed => True
  | _                       => False
  end.

#[export]
Instance compressionMethodDescribable : describable compressionMethod := {
  descriptorOf c := compressionMethodDescriptor c
}.

5.11. Calino/CoordinateSystem.v

Require Import Coq.Strings.String.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Inductive coordinateAxisR : Set :=
  | AxisRIncreasingToward
  | AxisRIncreasingAway.

Inductive coordinateAxisS : Set :=
  | AxisSIncreasingRight
  | AxisSIncreasingLeft.

Inductive coordinateAxisT : Set :=
  | AxisTIncreasingDown
  | AxisTIncreasingUp.

Definition coordinateAxisRDescribe (c : coordinateAxisR) : descriptor :=
  match c with
  | AxisRIncreasingToward => "RT"
  | AxisRIncreasingAway   => "RA"
  end.

Definition coordinateAxisSDescribe (c : coordinateAxisS) : descriptor :=
  match c with
  | AxisSIncreasingRight => "SR"
  | AxisSIncreasingLeft  => "SL"
  end.

Definition coordinateAxisTDescribe (c : coordinateAxisT) : descriptor :=
  match c with
  | AxisTIncreasingDown => "TD"
  | AxisTIncreasingUp   => "TU"
  end.

#[export]
Instance coordinateAxisRDescribable : describable coordinateAxisR := {
  descriptorOf c := coordinateAxisRDescribe c
}.

#[export]
Instance coordinateAxisSDescribable : describable coordinateAxisS := {
  descriptorOf c := coordinateAxisSDescribe c
}.

#[export]
Instance coordinateAxisTDescribable : describable coordinateAxisT := {
  descriptorOf c := coordinateAxisTDescribe c
}.

Inductive coordinateSystem : Set :=
  CoordinateSystem : coordinateAxisR → coordinateAxisS → coordinateAxisT → coordinateSystem.

Definition coordinateSystemDescribe (c : coordinateSystem) : descriptor :=
  match c with
  | CoordinateSystem r s t =>
    descriptorOf r ++ ":" ++ descriptorOf s ++ ":" ++ descriptorOf t
  end.

#[export]
Instance coordinateSystemDescribable : describable coordinateSystem := {
  descriptorOf c := coordinateSystemDescribe c
}.

5.12. Calino/CubeMipMap.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Bool.Bool.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.ImageSize.

Import ListNotations.

Inductive cubeMapFace : Set := CubeMapFace {
  cubeFaceOffset           : nat;
  cubeFaceSizeCompressed   : nat;
  cubeFaceSizeUncompressed : nat;
  cubeFaceCRC32            : nat
}.

Inductive cubeMipMap : Set := CubeMipMap {
  cubeMapLevel     : nat;
  cubeMapFaceXPos  : cubeMapFace;
  cubeMapFaceXNeg  : cubeMapFace;
  cubeMapFaceYPos  : cubeMapFace;
  cubeMapFaceYNeg  : cubeMapFace;
  cubeMapFaceZPos  : cubeMapFace;
  cubeMapFaceZNeg  : cubeMapFace
}.

Definition cubeFaceExtent (f : cubeMapFace) : nat :=
  cubeFaceOffset f + cubeFaceSizeCompressed f.

Inductive cubeOffsetsSorted : list cubeMipMap → Prop :=
  | CMMSizeOne  : ∀ m,
    cubeFaceExtent (cubeMapFaceXPos m) < cubeFaceOffset (cubeMapFaceXNeg m) →
    cubeFaceExtent (cubeMapFaceXNeg m) < cubeFaceOffset (cubeMapFaceYPos m) →
    cubeFaceExtent (cubeMapFaceYPos m) < cubeFaceOffset (cubeMapFaceYNeg m) →
    cubeFaceExtent (cubeMapFaceYNeg m) < cubeFaceOffset (cubeMapFaceZPos m) →
    cubeFaceExtent (cubeMapFaceZPos m) < cubeFaceOffset (cubeMapFaceZNeg m) →
      cubeOffsetsSorted [m]
  | CMMSizeCons : ∀ mm0 mm1 mxs,
    cubeFaceExtent (cubeMapFaceZNeg mm1) < cubeFaceOffset (cubeMapFaceXPos mm0) →
      cubeOffsetsSorted (mm0 :: mxs) →
        cubeOffsetsSorted (mm1 :: mm0 :: mxs).

Inductive cubeMipMapListIsSorted : list cubeMipMap → Prop :=
  | CubeOne   : ∀ m, cubeMipMapListIsSorted [m]
  | CubeCons  : ∀ mm0 mm1 mxs,
    cubeMapLevel mm1 = S (cubeMapLevel mm0) →
      cubeMipMapListIsSorted (mm0 :: mxs) →
        cubeMipMapListIsSorted (mm1 :: mm0 :: mxs).

Inductive cubeMipMapList : Set := CubeList {
  cubeMipMaps              : list cubeMipMap;
  cubeMipMapsListSorted    : cubeMipMapListIsSorted cubeMipMaps;
  cubeMipMapsOffsetsSorted : cubeOffsetsSorted cubeMipMaps;
}.

Lemma cubeMipMapsNonEmpty : ∀ (m : cubeMipMapList),
  [] ≠ cubeMipMaps m.
Proof.
  intros m.
  destruct (cubeMipMapsOffsetsSorted m).
  - discriminate.
  - discriminate.
Qed.

Definition cubeMipMapsFirst (m : cubeMipMapList) : cubeMipMap.
Proof.
  assert ([] ≠ cubeMipMaps m) as Hneq by (apply (cubeMipMapsNonEmpty)).
  destruct (cubeMipMaps m) eqn:Hm.
  - contradiction.
  - exact c.
Defined.

Fixpoint cubeMipMapImageDataSizeTotalAux (m : list cubeMipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => cubeFaceExtent (cubeMapFaceZNeg x)
  | (x :: xs) => cubeMipMapImageDataSizeTotalAux xs
  end.

Definition cubeMipMapImageDataSizeTotal (m : cubeMipMapList) : nat :=
  cubeMipMapImageDataSizeTotalAux (cubeMipMaps m).

Example cubeFaceXP0 := CubeMapFace 0 8 8 0.
Example cubeFaceXN0 := CubeMapFace 16 8 8 0.
Example cubeFaceYP0 := CubeMapFace 32 8 8 0.
Example cubeFaceYN0 := CubeMapFace 48 8 8 0.
Example cubeFaceZP0 := CubeMapFace 64 8 8 0.
Example cubeFaceZN0 := CubeMapFace 80 8 8 0.

Example cubeMipMap0 := CubeMipMap 1 cubeFaceXP0 cubeFaceXN0 cubeFaceYP0 cubeFaceYN0 cubeFaceZP0 cubeFaceZN0.

Example cubeFaceXP1 := CubeMapFace 96 8 8 0.
Example cubeFaceXN1 := CubeMapFace 112 8 8 0.
Example cubeFaceYP1 := CubeMapFace 128 8 8 0.
Example cubeFaceYN1 := CubeMapFace 144 8 8 0.
Example cubeFaceZP1 := CubeMapFace 160 8 8 0.
Example cubeFaceZN1 := CubeMapFace 176 8 8 0.

Example cubeMipMap1 := CubeMipMap 0 cubeFaceXP1 cubeFaceXN1 cubeFaceYP1 cubeFaceYN1 cubeFaceZP1 cubeFaceZN1.

Example cubeOffsetsSortedExample0 : cubeOffsetsSorted [cubeMipMap0].
Proof.
  apply CMMSizeOne.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
Qed.

Example cubeOffsetsSortedExample1 : cubeOffsetsSorted [cubeMipMap1].
Proof.
  apply CMMSizeOne.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
  compute; repeat constructor.
Qed.

Example cubeOffsetsSortedExample2 : cubeOffsetsSorted [cubeMipMap0; cubeMipMap1].
Proof.
  apply CMMSizeCons.
  compute; repeat constructor.
  exact cubeOffsetsSortedExample1.
Qed.

Example cubeLevelSortedExample0 : cubeMipMapListIsSorted [cubeMipMap0].
Proof.
  apply CubeOne.
Qed.

Example cubeLevelSortedExample1 : cubeMipMapListIsSorted [cubeMipMap1].
Proof.
  apply CubeOne.
Qed.

Example cubeLevelSortedExample2 : cubeMipMapListIsSorted [cubeMipMap0; cubeMipMap1].
Proof.
  apply CubeCons.
  reflexivity.
  apply CubeOne.
Qed.

5.13. Calino/Descriptor.v

Require Import Coq.Strings.String.
Require Import Coq.Strings.Ascii.

Open Scope string_scope.
Open Scope char_scope.

Definition descriptor := string.

Class describable (A : Set) := {
  descriptorOf : A -> descriptor
}.

5.14. Calino/Divisible8.v

Require Import Coq.PArith.PArith.
Require Import Coq.Arith.PeanoNat.
Require Import Coq.Init.Nat.
Require Import Coq.Lists.List.
Require Import Coq.Unicode.Utf8_core.

(* Set Mangle Names. *)

Definition divisible8 (x : nat) : Prop :=
  modulo x 8 = 0.

Theorem divisiblityNAdd : ∀ (x y z : nat),
  0 ≠ z → x mod z = 0 → y mod z = 0 → (x + y) mod z = 0.
Proof.
  intros x y z Hz Hx Hy.
  destruct y as [|y].
    (* If y = 0, then this matches one of our assumptions already. *)
    rewrite Nat.add_0_r; exact Hx.
    (* Otherwise, the following property always holds given that the divisor is ≠ 0. *)
    assert ((x mod z + S y) mod z = (x + S y) mod z) as Heq.
      apply (Nat.add_mod_idemp_l x (S y) z).
      apply (Nat.neq_sym 0 z Hz).
    (* x mod z = 0 *)
    rewrite Hx in Heq.
    (* 0 + S y = S y *)
    rewrite Nat.add_0_l in Heq.
    rewrite <- Heq.
    exact Hy.
Qed.

Theorem divisibilityNFoldPlus : ∀ z xs,
  0 ≠ z →
    Forall (λ n, n mod z = 0) xs →
      (fold_right plus 0 xs) mod z = 0.
Proof.
  intros z xs Hnz HforAll.
  induction xs as [|y ys].
  - apply (Nat.mod_0_l z (Nat.neq_sym 0 z Hnz)).
  - assert (fold_right add 0 (y :: ys) = y + fold_right add 0 ys) as Hfoldeq by reflexivity.
    rewrite Hfoldeq.
    assert (fold_right add 0 ys mod z = 0) as Hfoldeq2. {
      apply IHys.
      apply (@Forall_inv_tail nat (λ n : nat, n mod z = 0) y ys HforAll).
    }
    rewrite divisiblityNAdd.
    reflexivity.
    exact Hnz.
    apply (@Forall_inv nat (λ n : nat, n mod z = 0) y ys HforAll).
    exact Hfoldeq2.
Qed.

Theorem divisiblity8Add : ∀ (x y : nat),
  divisible8 x → divisible8 y → divisible8 (x + y).
Proof.
  intros x y Hx Hy.
  unfold divisible8 in *.
  apply divisiblityNAdd.
  discriminate.
  trivial.
  trivial.
Qed.

5.15. Calino/Flag.v

Require Import Coq.Strings.String.
Require Import Coq.Lists.List.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Import ListNotations.

Inductive flag : Set :=
  | FlagAlphaPremultiplied
  | FlagCustom : descriptor → flag.

Definition flagDescribe (f : flag) : descriptor :=
  match f with
  | FlagAlphaPremultiplied => "ALPHA_PREMULTIPLIED"
  | FlagCustom d           => d
  end.

#[export]
Instance flagDescribable : describable flag := {
  descriptorOf f := flagDescribe f
}.

Inductive flagSet : Set := {
  flags      : list flag;
  flagsNoDup : NoDup flags;
}.

5.16. Calino/ImageInfo.v

Require Import Coq.PArith.PArith.
Require Import Coq.Arith.PeanoNat.
Require Import Coq.Program.Basics.
Require Import Coq.Strings.String.
Require Import Coq.Strings.Ascii.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Divisible8.
Require Import Calino.StringUtility.
Require Import Calino.Descriptor.
Require Import Calino.ChannelDescription.
Require Import Calino.ChannelSemantic.
Require Import Calino.ChannelType.
Require Import Calino.Compression.
Require Import Calino.SuperCompression.
Require Import Calino.ColorSpace.
Require Import Calino.Flag.
Require Import Calino.ByteOrder.
Require Import Calino.CoordinateSystem.
Require Import Calino.ImageSize.

Open Scope program_scope.

Record imageInfo : Set := ImageInfo {
  imageSize                   : imageSize3D;
  imageChannelsLayout         : channelLayoutDescription;
  imageChannelsType           : channelType;
  imageCompressionMethod      : compressionMethod;
  imageSuperCompressionMethod : superCompressionMethod;
  imageCoordinateSystem       : coordinateSystem;
  imageColorSpace             : colorSpace;
  imageFlags                  : flagSet;
  imageByteOrder              : byteOrder
}.

Definition imageSizeX :=
  sizeX ∘ imageSize.

Definition imageSizeY :=
  sizeY ∘ imageSize.

Definition imageSizeZ :=
  sizeZ ∘ imageSize.

Definition imageFlagSet :=
  flags ∘ imageFlags.

Definition imageInfoTexelBlockAlignment (i : imageInfo) :=
  let c := imageCompressionMethod i in
    match c with
    | CompressionUncompressed => channelLayoutDescriptionBits (imageChannelsLayout i) / 8
    | _                       => compressionBlockAlignment c
    end.

Theorem imageInfoTexelBlockAlignmentPositive : ∀ i,
  0 < imageInfoTexelBlockAlignment i.
Proof.
  intros i.
  unfold imageInfoTexelBlockAlignment.
  destruct (imageCompressionMethod i) eqn:Hm.
  - assert (8 <= channelLayoutDescriptionBits (imageChannelsLayout i)) as Hle8
      by (apply (channelLayoutDescriptionBitsLe8)).
    apply (Nat.div_le_lower_bound (channelLayoutDescriptionBits (imageChannelsLayout i)) 8 1).
    discriminate.
    rewrite Nat.mul_1_r.
    exact Hle8.
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - repeat (constructor).
  - auto.
Qed.

Theorem imageInfoTexelBlockAlignmentNonZero : ∀ i,
  0 ≠ imageInfoTexelBlockAlignment i.
Proof.
  intros i.
  apply Lt.lt_0_neq.
  apply imageInfoTexelBlockAlignmentPositive.
Qed.

5.17. Calino/ImageSize.v

Require Import Coq.Unicode.Utf8_core.

Record imageSize3D : Set := ImageSize3D {
  sizeX     : nat;
  sizeY     : nat;
  sizeZ     : nat;
  sizeXnot0 : 0 ≠ sizeX;
  sizeYnot0 : 0 ≠ sizeY;
  sizeZnot0 : 0 ≠ sizeZ;
}.

5.18. Calino/Metadata.v

Require Import Coq.Strings.String.
Require Import Coq.Strings.Ascii.
Require Import Coq.Lists.List.
Require Import Coq.Unicode.Utf8_core.

Open Scope string_scope.

Import ListNotations.

Inductive metadataValue : Set := MetadataValue {
  mKey   : string;
  mValue : string
}.

Inductive metadata : Set := Metadata {
  mValues : list metadataValue
}.

5.19. Calino/MipMap.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Lists.List.
Require Import Coq.Init.Nat.
Require Import Coq.Bool.Bool.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.ImageSize.

Import ListNotations.

Inductive mipMap : Set := MipMap {
  mipMapLevel            : nat;
  mipMapOffset           : nat;
  mipMapSizeCompressed   : nat;
  mipMapSizeUncompressed : nat;
  mipMapCRC32            : nat
}.

Inductive mipMapListIsSorted : list mipMap → Prop :=
  | MipsOne   : ∀ m, mipMapListIsSorted [m]
  | MipsCons  : ∀ mm0 mm1 mxs,
    mipMapLevel mm1 = S (mipMapLevel mm0) →
      mipMapListIsSorted (mm0 :: mxs) →
        mipMapListIsSorted (mm1 :: mm0 :: mxs).

Inductive mipMapOffsetsSorted : list mipMap → Prop :=
  | MMSizeOne  : ∀ m, mipMapOffsetsSorted [m]
  | MMSizeCons : ∀ mm0 mm1 mxs,
    ((mipMapOffset mm1) + (mipMapSizeCompressed mm1)) < (mipMapOffset mm0) →
      mipMapOffsetsSorted (mm0 :: mxs) →
        mipMapOffsetsSorted (mm1 :: mm0 :: mxs).

Inductive mipMapList : Set := MipMapList {
  mipMaps            : list mipMap;
  mipMapListSorted   : mipMapListIsSorted mipMaps;
  mipMapOffsetSorted : mipMapOffsetsSorted mipMaps;
}.

Inductive mipMapImageSize : Set := MipMapImageSize {
  mmSizeX      : nat;
  mmSizeY      : nat;
  mmSizeXRange : 1 < mmSizeX;
  mmSizeYRange : 1 < mmSizeY;
}.

Lemma mipMapsNonEmpty : ∀ (m : mipMapList),
  [] ≠ mipMaps m.
Proof.
  intros m.
  destruct (mipMapListSorted m).
  - discriminate.
  - discriminate.
Qed.

Definition mipMapFirst (m : mipMapList) : mipMap.
Proof.
  assert ([] ≠ mipMaps m) as Hneq by (apply (mipMapsNonEmpty)).
  destruct (mipMaps m) eqn:Hm.
  - contradiction.
  - exact m0.
Defined.

Lemma lt_neq : ∀ n, 0 ≠ n ↔ 0 < n.
Proof.
  intros n.
  constructor.
  - intro Hneq.
    induction n as [|k].
    -- unfold not in Hneq.
       assert (0 = 0) as Heq by reflexivity.
       contradiction.
    -- apply (Nat.lt_0_succ k).
  - intro Hneq.
    induction n as [|k].
    -- inversion Hneq.
    -- discriminate.
Qed.

Lemma lt_neq_0 : ∀ n, 0 ≠ n → 0 < n.
Proof.
  intros n Hneq.
  rewrite <- lt_neq; trivial.
Qed.

Lemma lt_neq_1 : ∀ n, 0 < n → 0 ≠ n.
Proof.
  intros n Hneq.
  rewrite lt_neq; trivial.
Qed.

Definition mipMapSize
  (level      : nat)
  (imageSize  : imageSize3D)
  (levelRange : 0 < level)
: option mipMapImageSize :=
  let sx := (sizeX imageSize) / 2 ^ level in
  let sy := (sizeY imageSize) / 2 ^ level in
    match (Nat.ltb_spec0 1 sx, Nat.ltb_spec0 1 sy) with
    | (ReflectT _ xt, ReflectT _ yt) => Some (MipMapImageSize sx sy xt yt)
    | (_, _)                         => None
    end.

Fixpoint mipMapImageDataSizeTotalAux (m : list mipMap) : nat :=
  match m with
  | []        => 0
  | (x :: []) => (mipMapOffset x) + (mipMapSizeCompressed x)
  | (x :: xs) => mipMapImageDataSizeTotalAux xs
  end.

Definition mipMapImageDataSizeTotal (m : mipMapList) : nat :=
  mipMapImageDataSizeTotalAux (mipMaps m).

5.20. Calino/StandardFormats.v

Require Import Coq.Lists.List.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.ChannelDescription.
Require Import Calino.ChannelSemantic.
Require Import Calino.ChannelType.

Import ListNotations.

Declare Scope Forall_scope.

Open Scope Forall_scope.

Definition p0n1  : 0 ≠ 1  := O_S 0.
Definition p0n4  : 0 ≠ 4  := O_S 3.
Definition p0n5  : 0 ≠ 5  := O_S 4.
Definition p0n6  : 0 ≠ 6  := O_S 5.
Definition p0n8  : 0 ≠ 8  := O_S 7.
Definition p0n16 : 0 ≠ 16 := O_S 15.
Definition p0n32 : 0 ≠ 32 := O_S 31.
Definition p0n64 : 0 ≠ 64 := O_S 63.

Definition A1 : channelDescription := channelDescriptionMake CSAlpha 1 p0n1.

Definition R5 : channelDescription := channelDescriptionMake CSRed   5 p0n5.
Definition G6 : channelDescription := channelDescriptionMake CSGreen 6 p0n6.
Definition B5 : channelDescription := channelDescriptionMake CSBlue  5 p0n5.

Definition G5 : channelDescription := channelDescriptionMake CSGreen 5 p0n5.

Definition R4 : channelDescription := channelDescriptionMake CSRed   4 p0n4.
Definition G4 : channelDescription := channelDescriptionMake CSGreen 4 p0n4.
Definition B4 : channelDescription := channelDescriptionMake CSBlue  4 p0n4.
Definition A4 : channelDescription := channelDescriptionMake CSAlpha 4 p0n4.

Definition R8 : channelDescription := channelDescriptionMake CSRed   8 p0n8.
Definition G8 : channelDescription := channelDescriptionMake CSGreen 8 p0n8.
Definition B8 : channelDescription := channelDescriptionMake CSBlue  8 p0n8.
Definition A8 : channelDescription := channelDescriptionMake CSAlpha 8 p0n8.

Definition R8_Div8 : channelDescriptionBitsDivisible8 R8 := eq_refl.
Definition G8_Div8 : channelDescriptionBitsDivisible8 G8 := eq_refl.
Definition B8_Div8 : channelDescriptionBitsDivisible8 B8 := eq_refl.
Definition A8_Div8 : channelDescriptionBitsDivisible8 A8 := eq_refl.

Definition R16 : channelDescription := channelDescriptionMake CSRed   16 p0n16.
Definition G16 : channelDescription := channelDescriptionMake CSGreen 16 p0n16.
Definition B16 : channelDescription := channelDescriptionMake CSBlue  16 p0n16.
Definition A16 : channelDescription := channelDescriptionMake CSAlpha 16 p0n16.

Definition R16_Div8 : channelDescriptionBitsDivisible8 R16 := eq_refl.
Definition G16_Div8 : channelDescriptionBitsDivisible8 G16 := eq_refl.
Definition B16_Div8 : channelDescriptionBitsDivisible8 B16 := eq_refl.
Definition A16_Div8 : channelDescriptionBitsDivisible8 A16 := eq_refl.

Definition R32 : channelDescription := channelDescriptionMake CSRed   32 p0n32.
Definition G32 : channelDescription := channelDescriptionMake CSGreen 32 p0n32.
Definition B32 : channelDescription := channelDescriptionMake CSBlue  32 p0n32.
Definition A32 : channelDescription := channelDescriptionMake CSAlpha 32 p0n32.

Definition R32_Div8 : channelDescriptionBitsDivisible8 R32 := eq_refl.
Definition G32_Div8 : channelDescriptionBitsDivisible8 G32 := eq_refl.
Definition B32_Div8 : channelDescriptionBitsDivisible8 B32 := eq_refl.
Definition A32_Div8 : channelDescriptionBitsDivisible8 A32 := eq_refl.

Definition R64 : channelDescription := channelDescriptionMake CSRed   64 p0n64.
Definition G64 : channelDescription := channelDescriptionMake CSGreen 64 p0n64.
Definition B64 : channelDescription := channelDescriptionMake CSBlue  64 p0n64.
Definition A64 : channelDescription := channelDescriptionMake CSAlpha 64 p0n64.

Definition R64_Div8 : channelDescriptionBitsDivisible8 R64 := eq_refl.
Definition G64_Div8 : channelDescriptionBitsDivisible8 G64 := eq_refl.
Definition B64_Div8 : channelDescriptionBitsDivisible8 B64 := eq_refl.
Definition A64_Div8 : channelDescriptionBitsDivisible8 A64 := eq_refl.

(* Packed channels *)

Definition A1_R5_G5_B5_Channels : list channelDescription := [A1; R5; G5; B5].
Definition A1_R5_G5_B5_NonEmpty := nil_cons (x := A1) (l := [R5; G5; B5]).

Definition R4_G4_B4_A4_Channels : list channelDescription := [R4; G4; B4; A4].
Definition R4_G4_B4_A4_NonEmpty := nil_cons (x := R4) (l := [G4; B4; A4]).

Definition R5_G6_B5_Channels : list channelDescription := [R5; G6; B5].
Definition R5_G6_B5_NonEmpty := nil_cons (x := R5) (l := [G6; B5]).

(* 8-bit channels *)

Definition R8_G8_B8_A8_Channels : list channelDescription := [R8; G8; B8; A8].
Definition R8_G8_B8_A8_NonEmpty := nil_cons (x := R8) (l := [G8; B8; A8]).
Definition R8_G8_B8_A8_FDiv8 : Forall channelDescriptionBitsDivisible8 R8_G8_B8_A8_Channels :=
  Forall_cons R8 R8_Div8
 (Forall_cons G8 G8_Div8
 (Forall_cons B8 B8_Div8
 (Forall_cons A8 A8_Div8
 (Forall_nil _)))).

Definition R8_G8_B8_Channels : list channelDescription := [R8; G8; B8].
Definition R8_G8_B8_NonEmpty := nil_cons (x := R8) (l := [G8;B8]).
Definition R8_G8_B8_FDiv8 : Forall channelDescriptionBitsDivisible8 R8_G8_B8_Channels :=
  Forall_cons R8 R8_Div8
 (Forall_cons G8 G8_Div8
 (Forall_cons B8 B8_Div8
 (Forall_nil _))).

Definition R8_G8_Channels : list channelDescription := [R8; G8].
Definition R8_G8_NonEmpty := nil_cons (x := R8) (l := [G8]).
Definition R8_G8_FDiv8 : Forall channelDescriptionBitsDivisible8 R8_G8_Channels :=
  Forall_cons R8 R8_Div8
 (Forall_cons G8 G8_Div8
 (Forall_nil _)).

Definition R8_Channels : list channelDescription := [R8].
Definition R8_NonEmpty := nil_cons (x := R8) (l := []).
Definition R8_FDiv8 : Forall channelDescriptionBitsDivisible8 R8_Channels :=
  Forall_cons R8 R8_Div8 (Forall_nil _).

(* 16-bit channels *)

Definition R16_G16_B16_A16_Channels : list channelDescription := [R16; G16; B16; A16].
Definition R16_G16_B16_A16_NonEmpty := nil_cons (x := R16) (l := [G16; B16; A16]).
Definition R16_G16_B16_A16_FDiv8 : Forall channelDescriptionBitsDivisible8 R16_G16_B16_A16_Channels :=
  Forall_cons R16 R16_Div8
 (Forall_cons G16 G16_Div8
 (Forall_cons B16 B16_Div8
 (Forall_cons A16 A16_Div8
 (Forall_nil _)))).

Definition R16_G16_B16_Channels : list channelDescription := [R16; G16; B16].
Definition R16_G16_B16_NonEmpty := nil_cons (x := R16) (l := [G16;B16]).
Definition R16_G16_B16_FDiv8 : Forall channelDescriptionBitsDivisible8 R16_G16_B16_Channels :=
  Forall_cons R16 R16_Div8
 (Forall_cons G16 G16_Div8
 (Forall_cons B16 B16_Div8
 (Forall_nil _))).

Definition R16_G16_Channels : list channelDescription := [R16; G16].
Definition R16_G16_NonEmpty := nil_cons (x := R16) (l := [G16]).
Definition R16_G16_FDiv8 : Forall channelDescriptionBitsDivisible8 R16_G16_Channels :=
  Forall_cons R16 R16_Div8
 (Forall_cons G16 G16_Div8
 (Forall_nil _)).

Definition R16_Channels : list channelDescription := [R16].
Definition R16_NonEmpty := nil_cons (x := R16) (l := []).
Definition R16_FDiv8 : Forall channelDescriptionBitsDivisible8 R16_Channels :=
  Forall_cons R16 R16_Div8 (Forall_nil _).

(* 32-bit channels *)

Definition R32_G32_B32_A32_Channels : list channelDescription := [R32; G32; B32; A32].
Definition R32_G32_B32_A32_NonEmpty := nil_cons (x := R32) (l := [G32; B32; A32]).
Definition R32_G32_B32_A32_FDiv8 : Forall channelDescriptionBitsDivisible8 R32_G32_B32_A32_Channels :=
  Forall_cons R32 R32_Div8
 (Forall_cons G32 G32_Div8
 (Forall_cons B32 B32_Div8
 (Forall_cons A32 A32_Div8
 (Forall_nil _)))).

Definition R32_G32_B32_Channels : list channelDescription := [R32; G32; B32].
Definition R32_G32_B32_NonEmpty := nil_cons (x := R32) (l := [G32;B32]).
Definition R32_G32_B32_FDiv8 : Forall channelDescriptionBitsDivisible8 R32_G32_B32_Channels :=
  Forall_cons R32 R32_Div8
 (Forall_cons G32 G32_Div8
 (Forall_cons B32 B32_Div8
 (Forall_nil _))).

Definition R32_G32_Channels : list channelDescription := [R32; G32].
Definition R32_G32_NonEmpty := nil_cons (x := R32) (l := [G32]).
Definition R32_G32_FDiv8 : Forall channelDescriptionBitsDivisible8 R32_G32_Channels :=
  Forall_cons R32 R32_Div8
 (Forall_cons G32 G32_Div8
 (Forall_nil _)).

Definition R32_Channels : list channelDescription := [R32].
Definition R32_NonEmpty := nil_cons (x := R32) (l := []).
Definition R32_FDiv8 : Forall channelDescriptionBitsDivisible8 R32_Channels :=
  Forall_cons R32 R32_Div8 (Forall_nil _).

(* 64-bit channels *)

Definition R64_G64_B64_A64_Channels : list channelDescription := [R64; G64; B64; A64].
Definition R64_G64_B64_A64_NonEmpty := nil_cons (x := R64) (l := [G64; B64; A64]).
Definition R64_G64_B64_A64_FDiv8 : Forall channelDescriptionBitsDivisible8 R64_G64_B64_A64_Channels :=
  Forall_cons R64 R64_Div8
 (Forall_cons G64 G64_Div8
 (Forall_cons B64 B64_Div8
 (Forall_cons A64 A64_Div8
 (Forall_nil _)))).

Definition R64_G64_B64_Channels : list channelDescription := [R64; G64; B64].
Definition R64_G64_B64_NonEmpty := nil_cons (x := R64) (l := [G64;B64]).
Definition R64_G64_B64_FDiv8 : Forall channelDescriptionBitsDivisible8 R64_G64_B64_Channels :=
  Forall_cons R64 R64_Div8
 (Forall_cons G64 G64_Div8
 (Forall_cons B64 B64_Div8
 (Forall_nil _))).

Definition R64_G64_Channels : list channelDescription := [R64; G64].
Definition R64_G64_NonEmpty := nil_cons (x := R64) (l := [G64]).
Definition R64_G64_FDiv8 : Forall channelDescriptionBitsDivisible8 R64_G64_Channels :=
  Forall_cons R64 R64_Div8
 (Forall_cons G64 G64_Div8
 (Forall_nil _)).

Definition R64_Channels : list channelDescription := [R64].
Definition R64_NonEmpty := nil_cons (x := R64) (l := []).
Definition R64_FDiv8 : Forall channelDescriptionBitsDivisible8 R64_Channels :=
  Forall_cons R64 R64_Div8 (Forall_nil _).

(* Layouts *)

Definition Layout_A1_R5_G5_B5 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake A1_R5_G5_B5_Channels A1_R5_G5_B5_NonEmpty CLPack16 eq_refl).

Definition Layout_R4_G4_B4_A4 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake R4_G4_B4_A4_Channels R4_G4_B4_A4_NonEmpty CLPack16 eq_refl).

Definition Layout_R5_G6_B5 : channelLayoutDescription :=
  ChannelLayoutDescriptionPacked (CLDPMake R5_G6_B5_Channels R5_G6_B5_NonEmpty CLPack16 eq_refl).

Definition Layout_R8_G8_B8_A8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_B8_A8_Channels R8_G8_B8_A8_NonEmpty R8_G8_B8_A8_FDiv8).

Definition Layout_R8_G8_B8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_B8_Channels R8_G8_B8_NonEmpty R8_G8_B8_FDiv8).

Definition Layout_R8_G8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_G8_Channels R8_G8_NonEmpty R8_G8_FDiv8).

Definition Layout_R8 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R8_Channels R8_NonEmpty R8_FDiv8).

Definition Layout_R16_G16_B16_A16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_B16_A16_Channels R16_G16_B16_A16_NonEmpty R16_G16_B16_A16_FDiv8).

Definition Layout_R16_G16_B16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_B16_Channels R16_G16_B16_NonEmpty R16_G16_B16_FDiv8).

Definition Layout_R16_G16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_G16_Channels R16_G16_NonEmpty R16_G16_FDiv8).

Definition Layout_R16 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R16_Channels R16_NonEmpty R16_FDiv8).

Definition Layout_R32_G32_B32_A32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_B32_A32_Channels R32_G32_B32_A32_NonEmpty R32_G32_B32_A32_FDiv8).

Definition Layout_R32_G32_B32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_B32_Channels R32_G32_B32_NonEmpty R32_G32_B32_FDiv8).

Definition Layout_R32_G32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_G32_Channels R32_G32_NonEmpty R32_G32_FDiv8).

Definition Layout_R32 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R32_Channels R32_NonEmpty R32_FDiv8).

Definition Layout_R64_G64_B64_A64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_B64_A64_Channels R64_G64_B64_A64_NonEmpty R64_G64_B64_A64_FDiv8).

Definition Layout_R64_G64_B64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_B64_Channels R64_G64_B64_NonEmpty R64_G64_B64_FDiv8).

Definition Layout_R64_G64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_G64_Channels R64_G64_NonEmpty R64_G64_FDiv8).

Definition Layout_R64 : channelLayoutDescription :=
  ChannelLayoutDescriptionUnpacked (CLDUMake R64_Channels R64_NonEmpty R64_FDiv8).

5.21. Calino/StringUtility.v

Require Import Coq.Arith.PeanoNat.
Require Import Coq.Strings.String.
Require Import Coq.Strings.Ascii.

Open Scope string_scope.
Open Scope char_scope.

Set Mangle Names.

Definition digitOfNat (n : nat) : ascii :=
  match n with
  | 0 => "0"
  | 1 => "1"
  | 2 => "2"
  | 3 => "3"
  | 4 => "4"
  | 5 => "5"
  | 6 => "6"
  | 7 => "7"
  | 8 => "8"
  | _ => "9"
  end.

Fixpoint stringOfNatAux (time n : nat) (acc : string) : string :=
  let acc' := String (digitOfNat (n mod 10)) acc in
  match time with
  | 0 => acc'
  | S time' =>
    match n / 10 with
    | 0 => acc'
    | n' => stringOfNatAux time' n' acc'
    end
  end.

Definition stringOfNat (n : nat) : string :=
  stringOfNatAux n n "".

5.22. Calino/SuperCompression.v

Require Import Coq.Strings.String.
Require Import Coq.Unicode.Utf8_core.

Require Import Calino.Descriptor.

Inductive superCompressionMethod : Set :=
  | SuperCompressionUncompressed
  | SuperCompressionLZ4
  | SuperCompressionCustom : descriptor → nat → superCompressionMethod.

Definition superCompressionMethodDescriptor (c : superCompressionMethod) :=
  match c with
  | SuperCompressionUncompressed => "UNCOMPRESSED"
  | SuperCompressionLZ4          => "LZ4"
  | SuperCompressionCustom c _   => c
  end.

Definition superCompressionIsNotCompressed (c : superCompressionMethod) : Prop :=
  match c with
  | SuperCompressionUncompressed => True
  | _                            => False
  end.

Definition superCompressionSectionIdentifier (c : superCompressionMethod) : nat :=
  match c with
  | SuperCompressionUncompressed => 0
  | SuperCompressionLZ4          => 0
  | SuperCompressionCustom _ i   => i
  end.

#[export]
Instance superCompressionMethodDescribable : describable superCompressionMethod := {
  descriptorOf c := superCompressionMethodDescriptor c
}.

5.23. Calino/Texture.v

Require Import Coq.Unicode.Utf8_core.

Require Import Calino.CubeMipMap.
Require Import Calino.ArrayMipMap.
Require Import Calino.ImageInfo.
Require Import Calino.MipMap.

Inductive texture2d : Set := Texture2D {
  i2dInfo    : imageInfo;
  i2dMipMaps : mipMapList;
  i2dSize    : 1 = imageSizeZ i2dInfo
}.

Inductive textureArray : Set := TextureArray {
  iaInfo    : imageInfo;
  iaMipMaps : arrayMipMapList;
  iaSize    : 1 <= imageSizeZ iaInfo
}.

Inductive textureCube : Set := TextureCube {
  icubeInfo    : imageInfo;
  icubeMipMaps : cubeMipMapList;
  icubeSize    : 1 = imageSizeZ icubeInfo
}.

Inductive texture : Set :=
  | TTexture2D    : texture2d → texture
  | TTextureArray : textureArray → texture
  | TTextureCube  : textureCube → texture.

Definition imageInfoOf (i : texture) : imageInfo :=
  match i with
  | TTexture2D (Texture2D i _ _)       => i
  | TTextureArray (TextureArray i _ _) => i
  | TTextureCube (TextureCube i _ _)   => i
  end.
io7m | single-page | multi-page | epub | Calino 1.0