com.io7m.jcamera 0.6.0 Documentation

Regular releases are made to the Central Repository, so it's possible to use the com.io7m.jcamera package in your projects with the following Maven dependency:

<dependency>
  <groupId>com.io7m.jcamera</groupId>
  <artifactId>com.io7m.jcamera-core</artifactId>
  <version>0.6.0</version>
</dependency>

All io7m.com packages use Semantic Versioning [0] , which implies that it is always safe to use version ranges with an exclusive upper bound equal to the next major version - the API of the package will not change in a backwards-incompatible manner before the next major version.

1.3

Platform Specific Issues

There are currently no known platform-specific issues.

1.4

License

All files distributed with the com.io7m.jcamera package are placed under the following license:

Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com

Permission to use, copy, modify, and/or distribute this software for any
purpose with or without fee is hereby granted, provided that the above
copyright notice and this permission notice appear in all copies.

THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR
ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF
OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.

Usage

2.1. Usage
- 2.1.1. Overview
2.2. First-person camera
2.3. Example sources

2.1

Usage

2.1.1. Overview

2.1.1

Overview

This section attempts to describe how to use the com.io7m.jcamera package. The example code uses JOGL but the package can obviously be used under any Java input/windowing system. This section doesn't attempt to explain why anything works the way it does - readers are encouraged to read the design and implementation section, which describes everything in extensive detail.

A complete listing of all example source files is available at the end of the section.

2.2

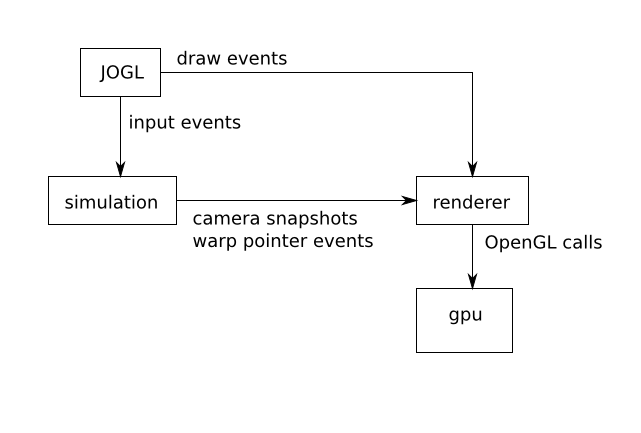
First-person camera

2.2.1. Overview
2.2.2. FPS Simulation
2.2.3. Input
2.2.4. Rendering/Interpolation
2.2.5. Main

2.2.1

Overview

In order to aid comprehension, and to follow good software engineering practices, the usage example here will be developed as a set of types with well-defined interfaces. Specifically, a simple main program will initialize an OpenGL window with JOGL, and register some keyboard and mouse listeners to supply input to a simulation, which in turn periodically produces new data (a view matrix) for a renderer. The renderer draws a simple static scene using the view matrix periodically produced by a camera from the com.io7m.jcamera package. The simulation runs at a fixed time step to provide completely frame rate independent movement (see the article "Fix Your Timestep!" for details on why physical simulations should use fixed time steps). The renderer, however, runs at an arbitrary frame rate. On some systems the frame rate will be exactly equal to the screen's vertical refresh rate, whilst on others, the rate will be thousands of times per second. The desire is to show that the system works equally well no matter what frame rate is used, so no attempt is made to enforce any particular rate. A rough graph of the data flow between components is as follows:

2.2.1.1. Example data flow

JOGL works with an event-based model, where mouse and keyboard input causes events to be delivered to mouse and keyboard listeners. Additionally, OpenGL rendering typically occurs via an OpenGL listener: JOGL (or the GPU, or the operating system, whichever is responsible) indicates that it is time to render the scene, and the user's registered listener is executed to actually perform the drawing. It's reasonable to assume that input handling and rendering occur on different threads by default, so the code here is careful to operate in a thread-safe manner.

The interface exposed to JOGL by the example renderer is as follows [ ExampleRendererType.java]:

2.2.1.2. Renderer interface

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

import com.io7m.jcamera.JCameraReadableSnapshotType;
import com.io7m.jtensors.core.unparameterized.vectors.Vector3D;
import com.jogamp.newt.opengl.GLWindow;
import com.jogamp.opengl.GL3;

import java.io.IOException;
import java.util.Optional;

/**
 * The interface exposed by the renderer to JOGL.
 */

public interface ExampleRendererType extends ExampleRendererControllerType
{
  /**
   * Initialize the scene, using the given window and OpenGL interface.
   *
   * @param in_window The window
   * @param in_gl     The OpenGL interface
   *
   * @throws IOException On I/O errors
   */

  void init(
    GLWindow in_window,
    GL3 in_gl)
    throws IOException;

  /**
   * Draw the scene.
   *
   * @param s      A camera snapshot
   * @param target An optional target to be drawn
   */

  void draw(
    JCameraReadableSnapshotType s,
    Optional<Vector3D> target);

  /**
   * Indicate that the screen has been resized.
   *
   * @param width  The new width
   * @param height The new height
   */

  void reshape(
    int width,
    int height);
}

Little is needed in the way of explanation here. The renderer initializes the scene's resources when init is called (such as allocating memory on the GPU for mesh data, compiling shaders, etc). The renderer draws the scene whenever draw is called, and recalculates any internal resources that are dependent on the size of the window (such as the scene's projection matrix) when reshape is called.

The actual implementation of the renderer is of little interest here. It simply draws a hundred or so static quads from the perspective of whatever is the current view matrix. The implementation is given in ExampleRenderer and will not be referenced again.

2.2.2

FPS Simulation

The interface exposed to JOGL by the example simulation is as follows [ ExampleFPSStyleSimulationType.java]:

2.2.2.1. Simulation interface

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

import com.io7m.jcamera.JCameraFPSStyleInputType;
import com.io7m.jcamera.JCameraFPSStyleIntegratorType;
import com.io7m.jcamera.JCameraFPSStyleSnapshot;
import com.io7m.jcamera.JCameraFPSStyleType;

/**
 * The interface to simulations (with fps-style cameras) exposed to JOGL.
 */

public interface ExampleFPSStyleSimulationType
{
  /**
   * @return {@code true} if the camera is enabled.
   */

  boolean cameraIsEnabled();

  /**
   * Enable/disable the camera.
   *
   * @param b {@code true} if the camera should be enabled.
   */

  void cameraSetEnabled(
    boolean b);

  /**
   * @return The camera used for the simulation.
   */

  JCameraFPSStyleType getCamera();

  /**
   * @return The simulation delta time
   */

  float getDeltaTime();

  /**
   * @return The camera input
   */

  JCameraFPSStyleInputType getInput();

  /**
   * @return The integrator used for the camera.
   */

  JCameraFPSStyleIntegratorType getIntegrator();

  /**
   * @return A new camera snapshot
   */

  JCameraFPSStyleSnapshot integrate();
}

Again, little is needed in the way of explanation. The simulation provides a camera that can be enabled and disabled. If the camera is disabled, a simple fixed camera is used rather than having the camera be driven by keyboard and mouse input.

The simulation needs a way to periodically warp the mouse cursor to the center of the screen if the movable camera is enabled, so the renderer exposes the following interface to the simulation [ ExampleRendererControllerType.java]:

2.2.2.2. Renderer control interface

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

/**
 * The interface that the simulation uses to talk to the renderer.
 */

public interface ExampleRendererControllerType
{
  /**
   * Tell the renderer/windowing system that it should warp the pointer to the
   * center of the screen.
   */

  void sendWantWarpPointer();
}

The actual implementation of the simulation is as follows [ ExampleFPSStyleSimulation.java]. First:

2.2.2.3. Camera declarations and storage

          /**
   * $example: Construct a new simulation.
   *
   * @param in_renderer The interface to the renderer
   */

  public ExampleFPSStyleSimulation(
    final ExampleRendererControllerType in_renderer)
  {
    this.renderer = in_renderer;
    this.input = JCameraFPSStyleInput.newInput();
    this.camera = JCameraFPSStyle.newCamera();
    final JCameraFPSStyleType camera_fixed = JCameraFPSStyle.newCamera();
    this.fixed_snapshot = JCameraFPSStyleSnapshots.of(camera_fixed);
    this.camera_enabled = new AtomicBoolean(false);

Then, an integrator is created to drive the camera, and the integration period required for a fixed time step of 60 frames per second is calculated:

2.2.2.4. Integrator

            /*
     * $example: Construct an integrator using the default implementations.
     */

    this.integrator =
      JCameraFPSStyleIntegrator.newIntegrator(this.camera, this.input);

    /*
     * Work out what fraction of a second the given simulation rate is going
     * to require.
     */

    final float rate = 60.0f;
    this.integrator_time_seconds = 1.0f / rate;

Finally, to give the camera somewhat more snappy and abrupt behaviour than the default settings, some new acceleration and drag values are configured for the camera:

2.2.2.5. Acceleration and Drag

            /*
     * $example: Configure the integrator. Use a high drag factor to give
     * quite abrupt stops, and use high rotational acceleration.
     */

    this.integrator.integratorAngularSetDragHorizontal(0.000000001);
    this.integrator.integratorAngularSetDragVertical(0.000000001);
    this.integrator.integratorAngularSetAccelerationHorizontal(
      Math.PI / 12.0 / (double) this.integrator_time_seconds);
    this.integrator.integratorAngularSetAccelerationVertical(
      Math.PI / 12.0 / (double) this.integrator_time_seconds);
    this.integrator.integratorLinearSetAcceleration(
      3.0 / (double) this.integrator_time_seconds);
    this.integrator.integratorLinearSetMaximumSpeed(3.0);
    this.integrator.integratorLinearSetDrag(0.000000001);
  }

The integrate function is executed at a rate of 60 times per second, and produces a new snapshot each time, which is passed to the renderer. The immutable nature of the snapshot means that it can be safely shared across threads without any need for locks or other synchronization. If the camera is actually enabled, the simulation also instructs the renderer to warp the mouse cursor back to the center of the screen. The rest of the functions complete the interface.

2.2.2.6. Integrate

          /**
   * $example: Integrate the camera.
   *
   * @return A new camera snapshot.
   */

  @Override
  public JCameraFPSStyleSnapshot integrate()
  {
    /*
     * If the camera is actually enabled, integrate and produce a snapshot,
     * and then tell the renderer/window system that it should warp the
     * pointer back to the center of the screen.
     */

    if (this.cameraIsEnabled()) {
      this.integrator.integrate(this.integrator_time_seconds);
      final JCameraFPSStyleSnapshot snap =
        JCameraFPSStyleSnapshots.of(this.camera);
      this.renderer.sendWantWarpPointer();
      return snap;
    }

    return this.fixed_snapshot;
  }

  @Override
  public boolean cameraIsEnabled()
  {
    return this.camera_enabled.get();
  }

  @Override
  public void cameraSetEnabled(
    final boolean b)
  {
    this.camera_enabled.set(b);
  }

  @Override
  public float getDeltaTime()
  {
    return this.integrator_time_seconds;
  }

  @Override
  public JCameraFPSStyleInputType getInput()
  {
    return this.input;
  }

  @Override
  public JCameraFPSStyleIntegratorType getIntegrator()
  {
    return this.integrator;
  }

  @Override
  public JCameraFPSStyleType getCamera()
  {
    return this.camera;
  }
}

2.2.3

Input

It's now necessary to supply the simulation with input.

A KeyListener is defined. Every time the user presses or releases a key, the simulation camera's input is notified accordingly.

There is one main issue covered here: If the user has keyboard auto-repeat enabled by their operating system, holding a key will result in an endless stream of "key pressed" and "key released" events. The code here is only interested in receiving the first "key pressed" and last "key released" event for each key, and JOGL's NEWT system marks each event as having been produced by auto-repeat (or not). Therefore, the auto-repeat flag is checked for each event, and the event is discarded if the flag is set.

Additionally, a few extra definitions allow for showing/hiding the mouse cursor, and switching between windowed and full-screen mode. JOGL requires that the setFullscreen function be called on a background thread, rather than the thread handling input and/or rendering for the current window.

2.2.3.1. Main (KeyListener)

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

import com.io7m.jcamera.JCameraFPSStyleInputType;
import com.jogamp.newt.event.InputEvent;
import com.jogamp.newt.event.KeyEvent;
import com.jogamp.newt.event.KeyListener;
import com.jogamp.newt.opengl.GLWindow;

import java.util.concurrent.ExecutorService;

/**
 * The key listener used to handle keyboard events.
 */

// CHECKSTYLE_JAVADOC:OFF

@SuppressWarnings("synthetic-access")
public final class ExampleFPSStyleKeyListener implements
  KeyListener
{
  private final ExampleFPSStyleSimulationType sim;
  private final ExecutorService background_workers;
  private final ExampleRendererType renderer;
  private final JCameraFPSStyleInputType input;
  private final GLWindow window;

  public ExampleFPSStyleKeyListener(
    final ExampleFPSStyleSimulationType in_sim,
    final ExecutorService in_background_workers,
    final ExampleRendererType in_renderer,
    final GLWindow in_window)
  {
    this.sim = in_sim;
    this.background_workers = in_background_workers;
    this.renderer = in_renderer;
    this.input = in_sim.getInput();
    this.window = in_window;
  }

  @Override
  public void keyPressed(
    final KeyEvent e)
  {
    assert e != null;

    /*
     * Ignore events that are the result of keyboard auto-repeat. This means
     * there's one single event when a key is pressed, and another when it is
     * released (as opposed to an endless stream of both when the key is held
     * down).
     */

    if ((e.getModifiers() & InputEvent.AUTOREPEAT_MASK) == InputEvent.AUTOREPEAT_MASK) {
      return;
    }

    switch (e.getKeyCode()) {

      /*
       * Standard WASD camera controls, with E and Q moving up and down,
       * respectively.
       */

      case KeyEvent.VK_A: {
        this.input.setMovingLeft(true);
        break;
      }
      case KeyEvent.VK_W: {
        this.input.setMovingForward(true);
        break;
      }
      case KeyEvent.VK_S: {
        this.input.setMovingBackward(true);
        break;
      }
      case KeyEvent.VK_D: {
        this.input.setMovingRight(true);
        break;
      }
      case KeyEvent.VK_E: {
        this.input.setMovingUp(true);
        break;
      }
      case KeyEvent.VK_Q: {
        this.input.setMovingDown(true);
        break;
      }
    }
  }

  @Override
  public void keyReleased(
    final KeyEvent e)
  {
    assert e != null;

    /*
     * Ignore events that are the result of keyboard auto-repeat. This means
     * there's one single event when a key is pressed, and another when it is
     * released (as opposed to an endless stream of both when the key is held
     * down).
     */

    if ((e.getModifiers() & InputEvent.AUTOREPEAT_MASK) == InputEvent.AUTOREPEAT_MASK) {
      return;
    }

    switch (e.getKeyCode()) {

      /*
       * Pressing 'M' enables/disables the camera.
       */

      case KeyEvent.VK_M: {
        this.toggleCameraEnabled();
        break;
      }

      /*
       * Pressing 'P' makes the mouse cursor visible/invisible.
       */

      case KeyEvent.VK_P: {
        System.out.printf(
          "Making pointer %s\n",
          this.window.isPointerVisible() ? "invisible" : "visible");
        this.window.setPointerVisible(!this.window.isPointerVisible());
        break;
      }

      /*
       * Pressing enter switches between windowed and fullscreen mode. JOGL
       * requires that this be executed on a background thread.
       */

      case KeyEvent.VK_ENTER: {
        this.background_workers.execute(new Runnable()
        {
          @Override
          public void run()
          {
            final boolean mode =
              !ExampleFPSStyleKeyListener.this.window.isFullscreen();
            ExampleFPSStyleKeyListener.this.window.setFullscreen(mode);
          }
        });
        break;
      }

      /*
       * Standard WASD camera controls, with E and Q moving up and down,
       * respectively.
       */

      case KeyEvent.VK_A: {
        this.input.setMovingLeft(false);
        break;
      }
      case KeyEvent.VK_W: {
        this.input.setMovingForward(false);
        break;
      }
      case KeyEvent.VK_S: {
        this.input.setMovingBackward(false);
        break;
      }
      case KeyEvent.VK_D: {
        this.input.setMovingRight(false);
        break;
      }
      case KeyEvent.VK_E: {
        this.input.setMovingUp(false);
        break;
      }
      case KeyEvent.VK_Q: {
        this.input.setMovingDown(false);
        break;
      }
    }
  }

  public void toggleCameraEnabled()
  {
    final boolean enabled = this.sim.cameraIsEnabled();

    if (enabled) {
      System.out.println("Disabling camera");
      this.window.confinePointer(false);
    } else {
      System.out.println("Enabling camera");
      this.window.confinePointer(true);
      this.renderer.sendWantWarpPointer();
      this.input.setRotationHorizontal(0.0);
      this.input.setRotationVertical(0.0);
    }

    this.sim.cameraSetEnabled(!enabled);
  }
}

A MouseAdapter is defined. Every time the user moves the mouse, the rotation coefficients are calculated and sent to the simulation camera's input:

2.2.3.2. Main (MouseAdapter)

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

import com.io7m.jcamera.JCameraFPSStyleInputType;
import com.io7m.jcamera.JCameraFPSStyleMouseRegion;
import com.io7m.jcamera.JCameraRotationCoefficientsMutable;
import com.jogamp.newt.event.MouseAdapter;
import com.jogamp.newt.event.MouseEvent;

import java.util.concurrent.atomic.AtomicReference;

/**
 * The mouse adapter used to handle mouse events.
 */

// CHECKSTYLE_JAVADOC:OFF

public final class ExampleFPSStyleMouseAdapter extends MouseAdapter
{
  private final AtomicReference<JCameraFPSStyleMouseRegion> mouse_region;
  private final JCameraFPSStyleInputType input;
  private final ExampleFPSStyleSimulationType sim;
  private final JCameraRotationCoefficientsMutable rotations;

  public ExampleFPSStyleMouseAdapter(
    final AtomicReference<JCameraFPSStyleMouseRegion> in_mouse_region,
    final ExampleFPSStyleSimulationType in_sim,
    final JCameraRotationCoefficientsMutable in_rotations)
  {
    this.mouse_region = in_mouse_region;
    this.input = in_sim.getInput();
    this.sim = in_sim;
    this.rotations = in_rotations;
  }

  @Override
  public void mouseMoved(
    final MouseEvent e)
  {
    assert e != null;

    /*
     * If the camera is enabled, get the rotation coefficients for the mouse
     * movement.
     */

    if (this.sim.cameraIsEnabled()) {
      this.rotations.from(
        this.mouse_region.get().coefficients(
          e.getX(),
          e.getY()));
      this.input.addRotationAroundHorizontal(this.rotations.horizontal());
      this.input.addRotationAroundVertical(this.rotations.vertical());
    }
  }
}

2.2.4

Rendering/Interpolation

A GLEventListener is added to the window. The listener will tell the renderer to draw the scene every time the OpenGL implementation requires a new frame.

The display method linearly interpolates between the most recently received camera snapshots in order to provide smooth animation independent of the simulation and/or frame rate.

2.2.4.1. Main (GLEventListener)

        /*
 * Copyright © 2021 Mark Raynsford <code@io7m.com> https://www.io7m.com
 *
 * Permission to use, copy, modify, and/or distribute this software for any
 * purpose with or without fee is hereby granted, provided that the above
 * copyright notice and this permission notice appear in all copies.
 *
 * THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES
 * WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF
 * MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY
 * SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
 * WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN
 * ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR
 * IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
 */

package com.io7m.jcamera.examples.jogl;

import com.io7m.jcamera.JCameraFPSStyleMouseRegion;
import com.io7m.jcamera.JCameraFPSStyleSnapshot;
import com.io7m.jcamera.JCameraFPSStyleSnapshots;
import com.io7m.jcamera.JCameraScreenOrigin;
import com.jogamp.newt.opengl.GLWindow;
import com.jogamp.opengl.DebugGL3;
import com.jogamp.opengl.GL;
import com.jogamp.opengl.GL3;
import com.jogamp.opengl.GLAutoDrawable;
import com.jogamp.opengl.GLEventListener;

import java.io.IOException;
import java.util.Optional;
import java.util.concurrent.atomic.AtomicReference;

/**
 * The GL event listener used to handle rendering and driving of the
 * simulation.
 */

// CHECKSTYLE_JAVADOC:OFF

public final class ExampleFPSStyleGLListener implements GLEventListener
{
  private final GLWindow window;
  private final ExampleFPSStyleSimulationType sim;
  private final AtomicReference<JCameraFPSStyleMouseRegion> mouse_region;
  private final ExampleRendererType renderer;
  private long time_then;
  private double time_accum;
  private JCameraFPSStyleSnapshot snap_curr;
  private JCameraFPSStyleSnapshot snap_prev;

  public ExampleFPSStyleGLListener(
    final GLWindow in_window,
    final JCameraFPSStyleSnapshot in_snap,
    final ExampleFPSStyleSimulationType in_sim,
    final AtomicReference<JCameraFPSStyleMouseRegion> in_mouse_region,
    final ExampleRendererType in_renderer)
  {
    this.window = in_window;
    this.sim = in_sim;
    this.mouse_region = in_mouse_region;
    this.renderer = in_renderer;
    this.snap_curr = in_snap;
    this.snap_prev = in_snap;
  }

  /**
   * Initialize the simulation.
   *
   * @param drawable The OpenGL drawable
   */

  @Override
  public void init(
    final GLAutoDrawable drawable)
  {
    try {
      assert drawable != null;

      final GL3 g = new DebugGL3(drawable.getGL().getGL3());
      assert g != null;

      this.time_then = System.nanoTime();
      this.renderer.init(this.window, g);
      this.renderer.reshape(this.window.getWidth(), this.window.getHeight());
    } catch (final IOException e) {
      throw new RuntimeException(e);
    }
  }

  @Override
  public void dispose(
    final GLAutoDrawable drawable)
  {
    // Nothing.
  }

  @Override
  public void display(
    final GLAutoDrawable drawable)
  {
    assert drawable != null;

    /*
     * Integrate the camera as many times as necessary for each rendering
     * frame interval.
     */

    final long time_now = System.nanoTime();
    final long time_diff = time_now - this.time_then;
    final double time_diff_s = (double) time_diff / 1000000000.0;
    this.time_accum = this.time_accum + time_diff_s;
    this.time_then = time_now;

    final float sim_delta = this.sim.getDeltaTime();
    while (this.time_accum >= (double) sim_delta) {
      this.snap_prev = this.snap_curr;
      this.snap_curr = this.sim.integrate();
      this.time_accum -= sim_delta;
    }

    /*
     * Determine how far the current time is between the current camera state
     * and the next, and use that value to interpolate between the two saved
     * states.
     */

    final float alpha = (float) (this.time_accum / (double) sim_delta);
    final JCameraFPSStyleSnapshot snap_interpolated =
      JCameraFPSStyleSnapshots.interpolate(
        this.snap_prev,
        this.snap_curr,
        alpha);

    final GL3 g = new DebugGL3(drawable.getGL().getGL3());
    assert g != null;
    g.glClear(GL.GL_COLOR_BUFFER_BIT);

    /*
     * Draw the scene!
     */

    this.renderer.draw(snap_interpolated, Optional.empty());
  }

  @Override
  public void reshape(
    final GLAutoDrawable drawable,
    final int x,
    final int y,
    final int width,
    final int height)
  {
    this.mouse_region.set(JCameraFPSStyleMouseRegion.of(
      JCameraScreenOrigin.SCREEN_ORIGIN_TOP_LEFT,
      width,
      height));
    this.renderer.reshape(width, height);
  }
}

2.2.5

Main

All that remains is to have JOGL tell the renderer when to render, and to supply the simulation with input in order to move and orient the camera according to mouse and keyboard input. The main program constructs a new renderer:

2.2.5.1. Main (Renderer)

            /*
     * $example: Construct a new renderer.
     */

    final ExampleRendererType renderer = new ExampleRenderer();

Then, a new simulation is constructed, and is passed a reference to the renderer (the type of the simulation constructor is declared such that it only sees a small subset of the interface exposed by the renderer). The simulation camera's input is also retrieved:

2.2.5.2. Main (Simulation)

            /*
     * $example: Construct a new simulation and produce an initial snapshot of
     * the camera for later use.
     */

    final ExampleFPSStyleSimulationType sim =
      new ExampleFPSStyleSimulation(renderer);
    final JCameraFPSStyleSnapshot snap = sim.integrate();

Some storage is allocated, and a mouse region is created to map mouse movements to rotational coefficients:

2.2.5.3. Main (Mouse region and coefficients)

            /*
     * $example: Declare a structure to hold mouse rotation coefficients, and
     * a mouse region configured with an origin that matches that of JOGL's
     * windowing system.
     */

    final JCameraRotationCoefficientsMutable rotations =
      JCameraRotationCoefficientsMutable.create();
    final AtomicReference<JCameraFPSStyleMouseRegion> mouse_region =
      new AtomicReference<>(
        JCameraFPSStyleMouseRegion.of(
          JCameraScreenOrigin.SCREEN_ORIGIN_TOP_LEFT,
          640.0,
          480.0));

An OpenGL window is created, an Animator is constructed that will tell the window to refresh frequently, and the previously defined listeners are attached to the window.

2.2.5.4. Main (Window and animator)

            /*
     * $example: Initialize JOGL and open a window, construct an animator to
     * regularly refresh the screen, and assign GL event listener, mouse
     * listener, and keyboard listener.
     */

    final GLProfile profile = GLProfile.get(GLProfile.GL3);
    final GLCapabilities caps = new GLCapabilities(profile);
    final GLWindow window = GLWindow.create(caps);
    window.setSize(640, 480);
    window.setTitle(ExampleFPSStyleMain.class.getCanonicalName());

    final Animator anim = new Animator();
    anim.add(window);

    window.addGLEventListener(new ExampleFPSStyleGLListener(
      window,
      snap,
      sim,
      mouse_region,
      renderer));

    window.addMouseListener(new ExampleFPSStyleMouseAdapter(
      mouse_region,
      sim,
      rotations));

    window.addKeyListener(new ExampleFPSStyleKeyListener(
      sim,
      background_workers,
      renderer,
      window));

    /*
     * Close the program when the window closes.
     */

    window.addWindowListener(new WindowAdapter()
    {
      @Override
      public void windowDestroyed(
        final WindowEvent e)
      {
        System.out.println("Stopping animator");
        anim.stop();
        System.out.println("Exiting");
        System.exit(0);
      }
    });

    window.setDefaultCloseOperation(
      WindowClosingProtocol.WindowClosingMode.DISPOSE_ON_CLOSE);
    window.setVisible(true);

    /*
     * Start everything running.
     */

    anim.start();
  }
}

2.2.5.5. Example screenshot

2.3

Example sources

The list of example source files:

2.3.1. Source files

Design And Implementation

3.1. Conventions
3.2. FPS Camera
3.3. Spherical Camera

3.1

Conventions

3.1.1. Overview
3.1.2. Architecture
3.1.3. Mathematics

3.1.1

Overview

This section attempts to document the mathematical and typographical conventions used in the rest of the documentation.

3.1.2

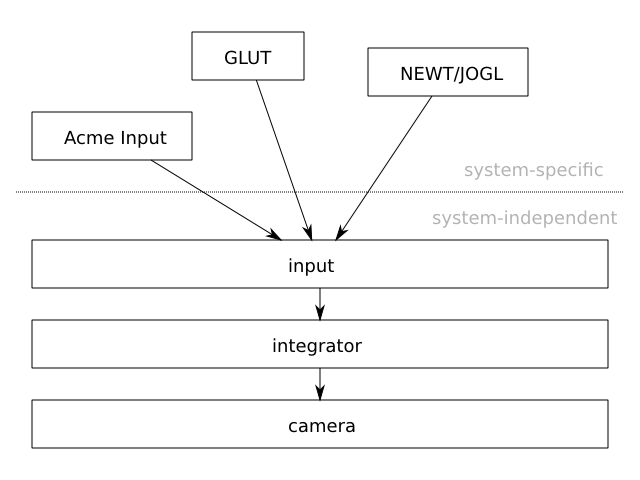
Architecture

The intention here is to first describe a simple purely mathematical rendering-and-input-system-independent camera that can be positioned and oriented, but that does not know anything about integration of its position and rotation over time. A separate system (the integrator) is built upon this camera that provides interpolation of the position and orientation over time to provide configurable smooth animation. Finally, a system (the input) is described that actually attaches the camera system to a keyboard and mouse package. The input package used in the examples is that of JOGL, but the system is specifically described in a manner to allow it to be easily adapted to any other input package. Essentially, the com.io7m.jcamera package tries to provide a cleanly-separated system-independent core, with the addition of a system to allow it to be attached to system-specific keyboard/mouse input packages. This is essential for the correctness of the software and also for the actual ease of understanding of the mathematics and implementation [1].

3.1.2.1. Architecture

3.1.3

Mathematics

Rather than rely on untyped and ambiguous mathematical notation, this documentation expresses all mathematics in strict Haskell 2010 with no extensions. All Haskell sources are included along with the documentation and can therefore be executed from the command line GHCi tool in order to interactively check results and experiment with functions.

When used within prose, functions are referred to using fully qualified notation, such as (Vector3f.cross n t). This an the application of the cross function defined in the Vector3f module, to the arguments n and t.

Formal examples and definitions, however, will typically be defined within their own modules, possibly with import statements used to allow for shorter names. As an example [ Forward.hs]:

3.1.3.1. Forward movement

        module Forward where

import qualified Vector3f

move_forward :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_forward p forward d = Vector3f.add3 p (Vector3f.scale forward d)

3.2

FPS Camera

3.2.1. Overview
3.2.2. Camera Behaviour
3.2.3. Camera Mathematics
3.2.4. Camera Implementation
3.2.5. Input
3.2.6. Integrators
3.2.7. Linear Integrators
3.2.8. Angular Integrators
3.2.9. Aggregate Integrators

3.2.1

Overview

Most modern 3D games and simulations feature a form of camera known, for want of a better name, as a first-person-shooter-style free-camera (subsequently referred to here as fps-style, for brevity). The camera is typically controlled by the combination of a mouse and keyboard and allows the user to orient the view direction using the mouse, and to move forwards, backwards, left, right, up, and down using the keyboard.

3.2.2

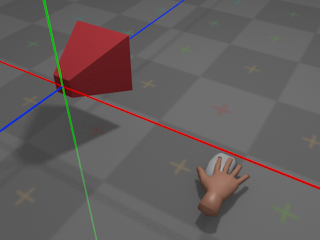
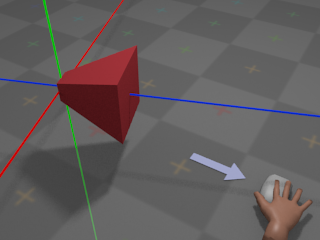
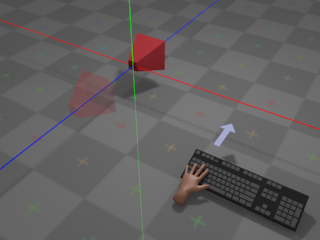
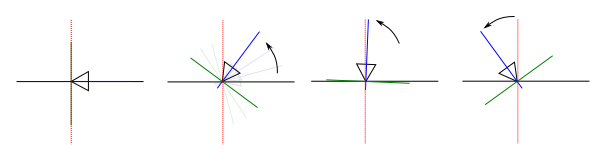
Camera Behaviour

With no input from the mouse, the camera remains at its current orientation:

3.2.2.1. No input

The green line denotes the camera's local Y axis, the red line denotes the camera's local X axis, and the blue line denotes the camera's local Z axis.

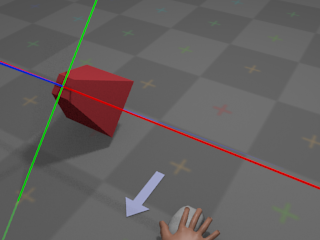
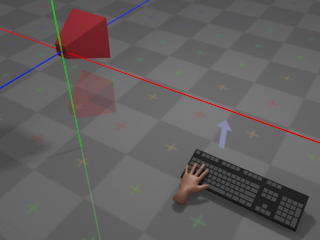
If the user moves the mouse left, the camera will rotate around the global Y axis and appear to turn left:

3.2.2.2. Mouse moves left

If the user moves the mouse right, the camera will rotate around the global Y axis and appear to turn right:

3.2.2.3. Mouse moves right

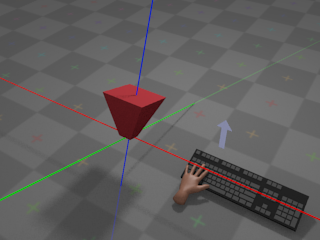
If the user pushes the mouse away, the camera will rotate around its own local X axis and appear to turn upwards:

3.2.2.4. Mouse moves away

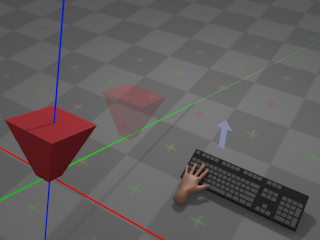
If the user pulls the mouse towards, the camera will rotate around its own local X axis and appear to turn downwards:

3.2.2.5. Mouse moves towards

The choice of whether towards and away mean "look down" and "look up", or "look up" and "look down", respectively, is a matter of personal taste. Most games and simulations provide an option to invert the Y axis for mouse control, so that moving the mouse away results in the camera turning downwards, and so on.

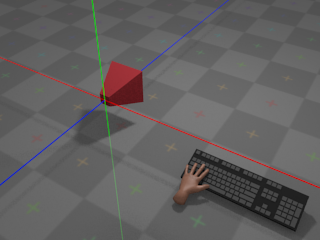
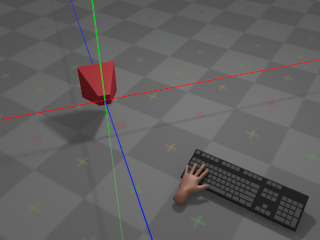
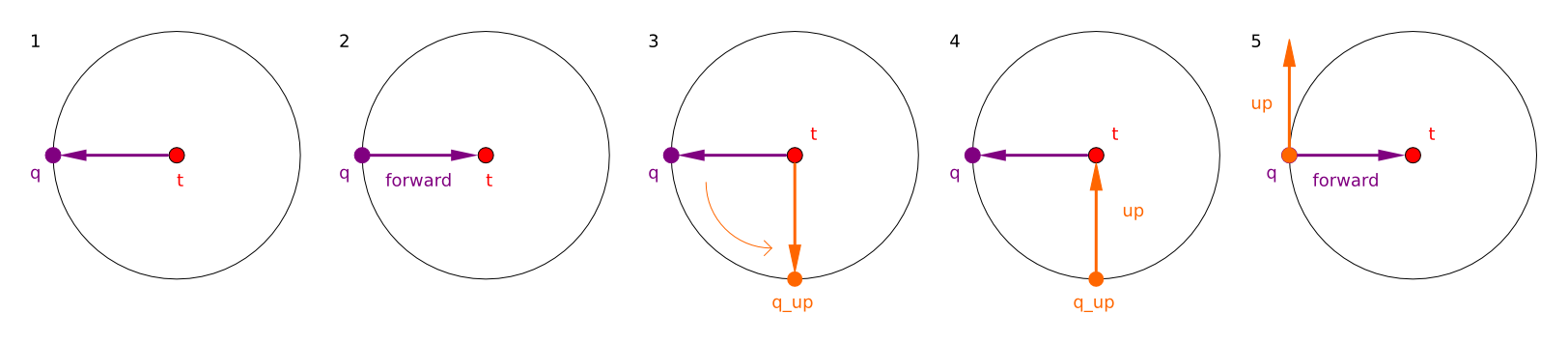
With no input from the keyboard, the camera remains at its current position:

3.2.2.6. No input

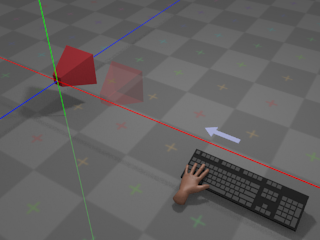
If the user presses whatever key is assigned to right, the camera moves towards positive infinity along its own local X axis at a configurable rate:

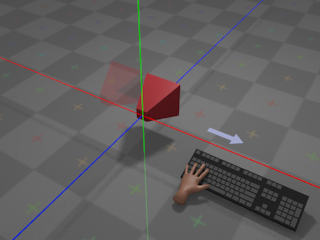
3.2.2.7. Keyboard right

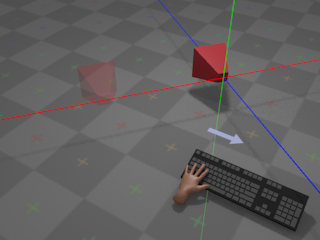
If the user presses whatever key is assigned to left, the camera moves towards negative infinity along its own local X axis at a configurable rate:

3.2.2.8. Keyboard left

Note that movement occurs along the local X axis; if the camera has been rotated around the global Y axis, then the local X axis has been transformed as a result, and movement will occur along a different trajectory than in the unrotated case:

3.2.2.9. Keyboard right (local 0)

3.2.2.10. Keyboard right (local 1)

If the user presses whatever key is assigned to forward, the camera moves towards negative infinity along its own local Z axis at a configurable rate:

3.2.2.11. Keyboard forward 0

3.2.2.12. Keyboard forward 1

Whether forward is considered to be towards positive or negative infinity on the Z axis is more or less a property of the coordinate system used by the rendering system. Systems such as OpenGL traditionally use a right-handed coordinate system, with forward pointing towards negative infinity. Systems such as Direct3D traditionally use a left-handed coordinate system, with forward pointing towards positive infinity. The com.io7m.jcamera package assumes a right-handed coordinate system.

As with movement on the local X axis, forward/backward movement occurs on the camera's local Z axis and is therefore affected by rotation around the Y axis.

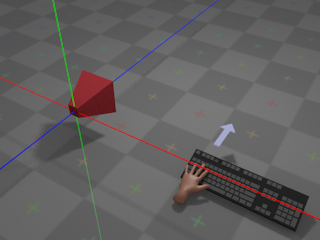
Finally, if the user presses whatever key is assigned to up, the camera moves towards positive infinity along its local Y axis (with down moving the camera towards negative infinity, accordingly):

3.2.2.13. Keyboard up 0

3.2.2.14. Keyboard up 1

Note that up and down movement occurs on the local Y axis and is therefore affected by the current orientation of the camera:

3.2.2.15. Keyboard up local 0

3.2.2.16. Keyboard up local 1

All other movement is restricted. The camera cannot, for example, rotate around its own local Z axis (the roll rotation, in aircraft terminology).

The rest of this section attempts to give a mathematical description of a camera system that implements the above behaviour, and describes the design and implementation of the camera system derived from the description as it exists in the com.io7m.jcamera package.

3.2.3

Camera Mathematics

An fps-style camera can be represented as a 3-tuple (p, h, v), where p is the position of the camera, h is an angle around the camera's local X axis in radians, and v is an angle around the global Y axis in radians. In order to implement forward/backward and left/right movement (and to derive a final view matrix so that the camera can be used to produce a viewing transform for 3D graphics), it's necessary to derive a 3-tuple of orthonormal direction vectors (forward, right, up) from the angles h and v.

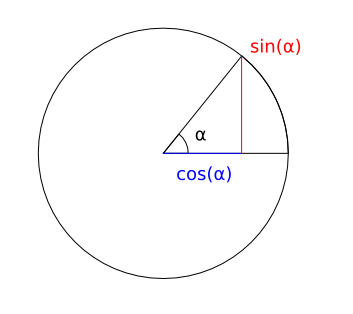
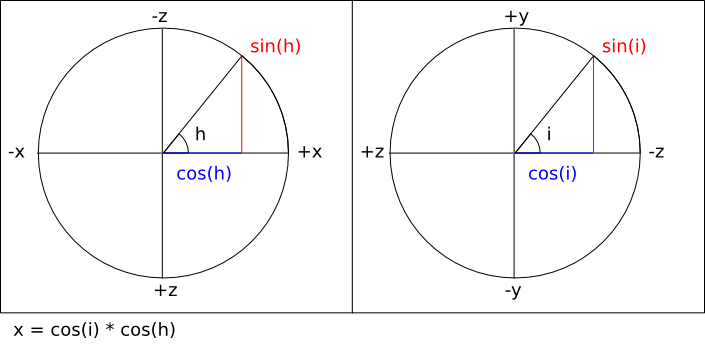
Given the standard trigonometric functions:

3.2.3.1. Trigonometric functions

It's possible to calculate the three components of the forward vector by assigning pairs of axes to the unit circle and using three equations:

3.2.3.2. Forward X

3.2.3.3. Forward Y

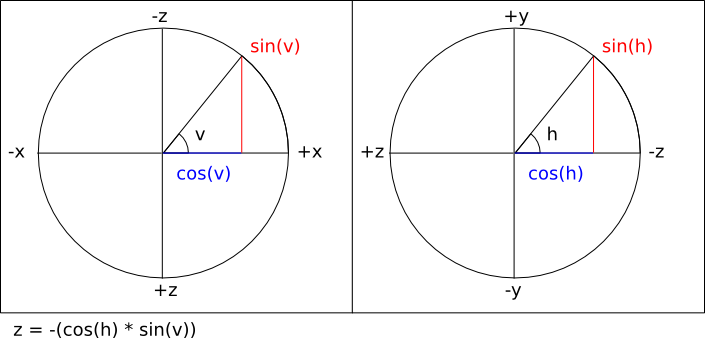
3.2.3.4. Forward Z

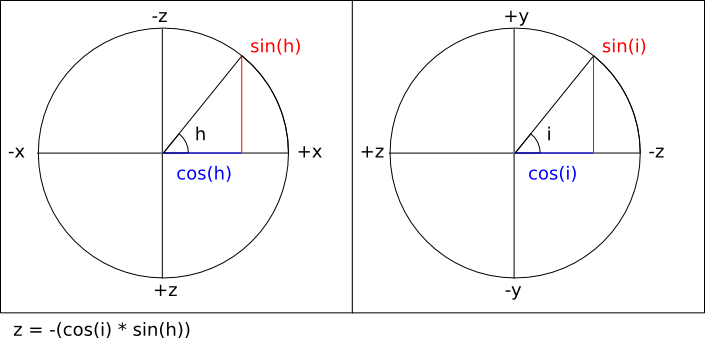
Note that the sign of the right hand side of the last equation is inverted in order to take into account the fact that the viewing direction is towards negative Z.

In most mathematics texts, a positive rotation around an axis represents a counter-clockwise rotation when viewing the system along the negative direction of the axis in question. Adhering to this convention, the equations for calculating the right vector are identical except for the fact that the equations work with a value of v - (π / 2) instead of v (a clockwise rotation of 90°).

Finally, calculating the up vector is simply a matter of calculating the cross product cross (right, forward).

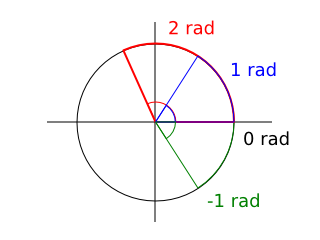
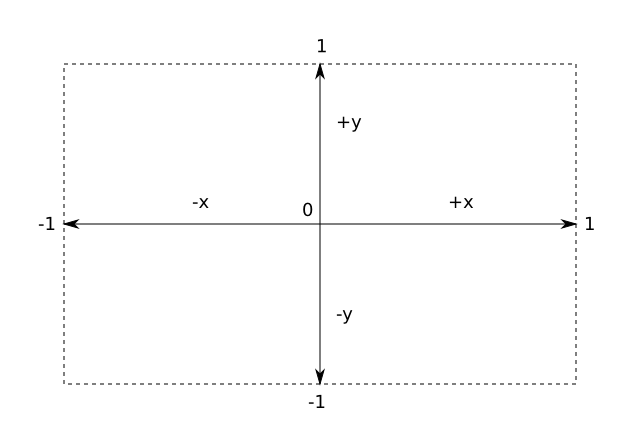
The com.io7m.jcamera package assumes that a camera with no rotation or translation applied is placed at the origin position p = (0, 0, 0) with h = 0 and v = π / 2. The reason for the value of v is that in most mathematics texts, an angle of 0 radians is illustrated as pointing to the right:

3.2.3.5. Angle convention

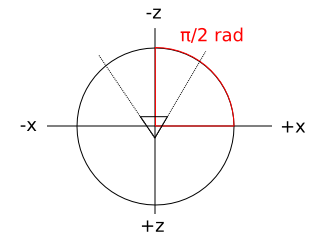
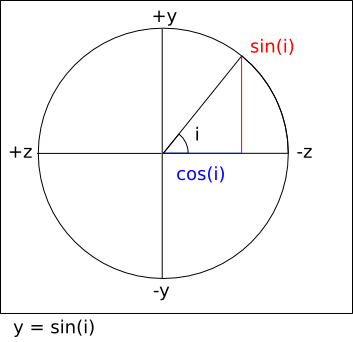
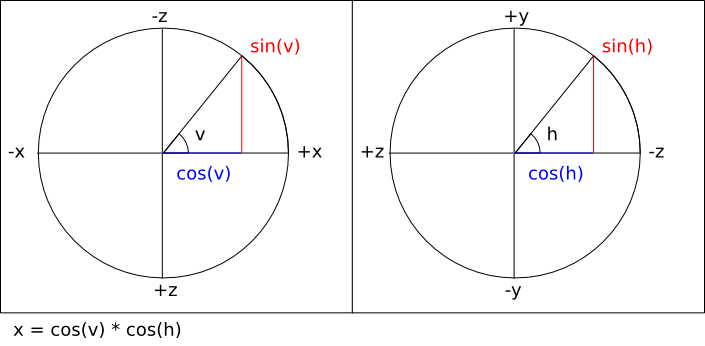
In a typical OpenGL configuration, the viewer is placed at the origin looking towards negative infinity on the Z axis, and the X axis appears to run horizontally, perpendicular to the viewing direction. Given this convention, it's somewhat intuitive to map those axes to the unit circle as follows (assuming a second observer looking down onto the scene towards negative infinity on the Y axis):

3.2.3.6. Angle convention (with axes)

Using this convention means that the values derived from the vector equations above can be used directly to compute a view matrix in the coordinate system conventionally used by OpenGL.

As a concrete example, using the default position and orientation given above, the resulting vectors are calculated as [ ExampleDefaultVectors.hs]:

3.2.3.7. Example default vectors

        module ExampleDefaultVectors where

import qualified Vector3f

h :: Float
h = 0

v :: Float
v = pi / 2.0

p :: Vector3f.T
p = Vector3f.V3 0.0 0.0 0.0

forward_x :: Float
forward_x = cos (v) * cos (h)
--        = cos (π / 2) * cos (0)
--        = 0 * 1
--        = 0

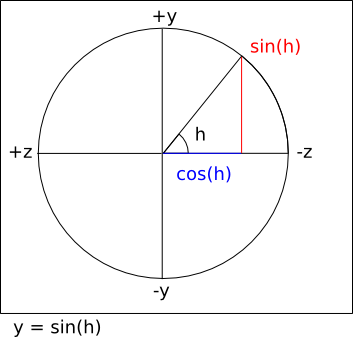
forward_y :: Float
forward_y = sin (h)
--        = sin (0)
--        = 0

forward_z :: Float
forward_z = -(cos (h) * sin (v))
--        = -(cos (0) * sin (π / 2))
--        = -(1 * 1)
--        = -1

forward :: Vector3f.T
forward = Vector3f.V3 forward_x forward_y forward_z
--      = (0, 0, -1)

right_x :: Float
right_x = cos (v - (pi / 2.0)) * cos (h)
--      = cos (0) * cos (0)
--      = 1 * 1
--      = 1

right_y :: Float
right_y = sin (h)
--      = sin (0)
--      = 0

right_z :: Float
right_z = -(cos (h) * sin (v - (pi / 2)))
--      = -(cos (0) * sin (0))
--      = -(1 * 0)
--      = 0

right :: Vector3f.T
right = Vector3f.V3 right_x right_y right_z
--    = (1, 0, 0)

up :: Vector3f.T
up = Vector3f.cross right forward
-- = ((right_y * forward_z) - (right_z * forward_y),
--    (right_z * forward_x) - (right_x * forward_z),
--    (right_x * forward_y) - (right_y * forward_x))
-- = ((0 * -1) - (0 * 0),
--    (0 * 0) - (1 * -1),
--    (1 * 0) - (0 * 0))
-- = (0, 1, 0)

The resulting forward, right, and up vectors are consistent with the Z, X, and Y axes typically used in OpenGL.

With the forward and right vectors calculated, it is now trivial to derive forward/backward and left/right movement. Forward movement by d units is simply a positive translation of the camera position p along the forward vector by d units [ Forward.hs]:

3.2.3.8. Forward movement

        module Forward where

import qualified Vector3f

move_forward :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_forward p forward d = Vector3f.add3 p (Vector3f.scale forward d)

A backward movement is simply the same equation with a negative d distance:

3.2.3.9. Backward movement

        module Backward where

import qualified Vector3f
import qualified Forward

move_backward :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_backward p forward d = Forward.move_forward p forward (-d)

Moving right is a positive translation of the camera position p along the right vector by d units:

3.2.3.10. Right movement

        module Right where

import qualified Vector3f

move_right :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_right p right d = Vector3f.add3 p (Vector3f.scale right d)

Moving left is simply the same equation with a negative d distance:

3.2.3.11. Left movement

        module Left where

import qualified Vector3f
import qualified Right

move_left :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_left p right d = Right.move_right p right (-d)

Moving up is a positive translation of the camera position p along the up vector by d units:

3.2.3.12. Up movement

        module Up where

import qualified Vector3f

move_up :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_up p up d = Vector3f.add3 p (Vector3f.scale up d)

Moving down is simply the same equation with a negative d distance:

3.2.3.13. Down movement

        module Down where

import qualified Vector3f
import qualified Up

move_down :: Vector3f.T -> Vector3f.T -> Float -> Vector3f.T
move_down p up d = Up.move_up p up (-d)

The right, up, and forward vectors form an orthonormal basis for a coordinate system. In practical terms, they provide the rotational component for a combined rotation and translation that can be used to transform arbitrary coordinates given in world space to eye space (also known as view space). This is what allows the camera system to actually be used as a camera in 3D simulations. A matrix that rotates vectors according to the calculated camera vectors is given by [ ViewRotation.hs]:

3.2.3.14. View matrix (rotation)

        module ViewRotation where

import qualified Matrix4f
import qualified Vector3f
import qualified Vector4f
import Vector3f (x, y, z)

rotation :: (Vector3f.T, Vector3f.T, Vector3f.T) -> Matrix4f.T
rotation (right, up, forward) =
  Matrix4f.T {
    Matrix4f.column_3 = Vector4f.V4  0.0         0.0         0.0        1.0,
    Matrix4f.column_2 = Vector4f.V4 (x forward) (y forward) (z forward) 0.0,
    Matrix4f.column_1 = Vector4f.V4 (x up)      (y up)      (z up)      0.0,
    Matrix4f.column_0 = Vector4f.V4 (x right)   (y right)   (z right)   0.0
  }

A matrix that translates vectors according to the current camera position is given by [ ViewTranslation.hs]:

3.2.3.15. View matrix (translation)

        module ViewTranslation where

import qualified Matrix4f
import qualified Vector3f
import qualified Vector4f
import Vector3f (x, y, z)

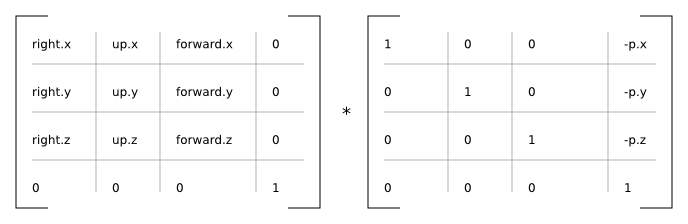
translation :: Vector3f.T -> Matrix4f.T
translation p =
  let np_x = -(x p)
      np_y = -(y p)
      np_z = -(z p)
  in
    Matrix4f.T {
      Matrix4f.column_3 = Vector4f.V4 np_x np_y np_z 1.0,
      Matrix4f.column_2 = Vector4f.V4 0.0  0.0  1.0  0.0,
      Matrix4f.column_1 = Vector4f.V4 0.0  1.0  0.0  0.0,
      Matrix4f.column_0 = Vector4f.V4 1.0  0.0  0.0  0.0
    }

The matrices are multiplied together, resulting in [View.hs]:

3.2.3.16. View matrix (complete)

        module View where

import ViewTranslation (translation)
import ViewRotation (rotation)
import qualified Matrix4f
import qualified Vector3f

view_matrix :: Vector3f.T -> (Vector3f.T, Vector3f.T, Vector3f.T) -> Matrix4f.T
view_matrix p (right, up, forward) =
  Matrix4f.mult (rotation (right, up, forward)) (translation p)

3.2.3.17. View matrix (diagram)

3.2.4

Camera Implementation

In the com.io7m.jcamera package, the interface exposed by an fps-style camera is described by the JCameraFPSStyleType type. The actual implementation of the camera mathematics is given in the JCameraFPSStyle type.

A small point to note about the implementation: The forward, right, and up vectors are calculated lazily whenever the user attempts to perform an operation that involves them. The vectors are derived only from the current camera angles and so are not recomputed if the angles have not been changed since the vectors were last calculated.

Additionally, the horizontal angle h can be clamped to a given range (and is clamped by default).

3.2.5

Input

In the com.io7m.jcamera package, an input is a simple abstraction intended to keep integrators insulated from the platform-specific details of keyboard and mouse input.

With the behaviour described in the first subsection, there are two types of input: Discrete input (where the user presses a key and the input is assumed to be constant until the key is released) and continuous input (where the user moves a mouse and a stream of new mouse position vectors are generated). Discrete input can be represented by a simple boolean flag, and continuous input can be represented by summing the received input until an integrator is ready to receive it.

An input in the com.io7m.jcamera package is represented by the following data structure [Input.hs]:

3.2.5.1. Input

        module Input (T (..)) where

data T = T {
  is_moving_backward  :: Bool,
  is_moving_forward   :: Bool,
  is_moving_left      :: Bool,
  is_moving_right     :: Bool,
  is_moving_up        :: Bool,
  is_moving_down      :: Bool,
  rotation_horizontal :: Float,
  rotation_vertical   :: Float
} deriving (Eq, Show)

When the user presses whatever is key assigned to up, the corresponding boolean field in the data structure is set to true. When the user releases the key, the corresponding field is set to false.

The situation for mouse movement is slightly more complex. Most OS-specific windowing systems will provide the user with the current mouse cursor coordinates as a pair of integer offsets (in pixels) relative to some origin. Some systems have the origin (0, 0) at the top-left corner of the screen/window, whilst others have it at the bottom-left corner of the window. Additionally, the density of displays is increasing at a steady rate. A monitor manufactured five years ago may be 40cm wide and have a resolution that fits 1440 pixels into that width. A modern display may be the same width but have over four times as many pixels in the same space. A camera system that recklessly consumes coordinates given in pixels is going to behave differently on a screen that has a higher density of pixels than it would on an older, lower resolution display.

In order for the com.io7m.jcamera package to remain system-independent, it's necessary to provide a way to map mouse input to a simple and consistent set of generic rotation coefficients that can be consumed by an integrator. The rotation coefficients are a pair of values (rx, ry) expressing the intention to rotate the camera, with rx affecting rotation around the camera's vertical axis, and ry affecting rotation around the camera's horizontal axis. In effect, when rx == -1.0, the camera should appear to rotate right [2] . When rx == 1.0, the camera should appear to rotate left. When ry == 1.0, the camera should appear to rotate up. When ry == -1.0, the camera should appear to rotate down. The coefficients linearly express fractional rotation, so a rotation of 0.5 is exactly half as much rotation as 1.0. The scheme used to map screen positions to coefficients is as follows:

3.2.5.2. Rotation coefficients

When the mouse cursor is in the exact center of the screen, the resulting rotation coefficients are (0, 0).
When the mouse cursor is in the uppermost, rightmost position of the screen q, the resulting rotation coefficients are (-1.0, 1.0).
When the mouse cursor is in the lowermost, leftmost position of the screen p, the resulting rotation coefficients are (1.0, -1.0).
The rotation coefficients for any other position on the screen can be derived from simple linear interpolation between p and q.

In order to actually map screen positions to rotation coefficients, it's necessary to take into account the windowing-system-specific origin. It's necessary to define a function that takes a mouse region representing the width and height of the screen with information labelling the origin, and a pair of screen/window-space coordinates (sx, sy), and returns a pair of rotation coefficients [ MouseRegion.hs]:

3.2.5.3. Mouse region

        module MouseRegion (T, newRegion, coefficients) where

data Origin =
    TopLeft
  | BottomLeft
    deriving (Eq, Show)

data T = T {
  origin   :: Origin,
  width    :: Float,
  height   :: Float,
  center_x :: Float,
  center_y :: Float
} deriving (Eq, Show)

newRegion :: Origin -> Float -> Float -> T
newRegion o w h = T {
  origin   = o,
  width    = w,
  height   = h,
  center_x = w / 2.0,
  center_y = h / 2.0
}

coefficients :: T -> (Integer, Integer) -> (Float, Float)
coefficients r (sx, sy) =
  let fx = fromIntegral sx
      fy = fromIntegral sy
      ox = ((fx - center_x r) / width r) * 2.0
      oy = ((fy - center_y r) / height r) * 2.0
  in
    case (origin r) of
      TopLeft    -> (-ox, -oy)
      BottomLeft -> (-ox, oy)

The assumption here is that the mouse cursor will be warped back to the center of the screen at periodic intervals. If this did not occur, the mouse cursor would eventually reach one or more edges of the screen and would be unable to travel further, halting any rotation in those directions.

In event-based windowing systems, every time the user moves the mouse, a mouse event is generated containing the current cursor position. In some systems, the user must explicitly ask for the current mouse position when it is needed. In the former case, new rotation coefficients will be generated repeatedly. In the latter case, the user will typically ask for the current mouse position at the beginning of rendering the current simulation frame, and therefore will only receive a single set of coefficients (effectively representing the furthest distance that the mouse travelled during that time period). In the com.io7m.jcamera package, an integrator will read (and reset to (0.0, 0.0)) the current rotation coefficients from an input at a (typically) fixed rate. The current rotation coefficients stored in an input therefore represent the sum of mouse movements for a given elapsed time period. To this end, the JCameraFPSStyleInput type in the com.io7m.jcamera package provides an interface where the user simply submits new rotation coefficients each time they are received, and the type keeps a running total of the coefficients. This allows the input system to work the same way regardless of whether the user has to ask for mouse input, or is receiving it piecemeal via some event system.

By taking the width and height of the screen in pixels, and dividing as shown in the above equations, the resulting coefficients are screen-density independent. In other words, if the user moves the cursor halfway across the screen on a very high density display, the resulting coefficients are the same as those resulting from a user moving the cursor across the same distance on a much lower density display, even though the distances expressed in pixels are very different.

In the com.io7m.jcamera package, fps-style inputs are represented by the JCameraFPSStyleInput type, and mouse regions are represented by the JCameraFPSStyleMouseRegion type.

3.2.6

Integrators

Integrators are responsible for updating properties of cameras over time. They are divided into linear and angular types.

3.2.7

Linear Integrators

A linear integrator updates the position of a camera over time.

In physics, the first derivative of position with respect to time is velocity. The second derivative of position with respect to time is acceleration. Newton's second law of motion relates force f with mass m and acceleration a [ SecondLaw.hs]:

3.2.7.1. Second Law

        module SecondLaw where

f :: Float -> Float -> Float
f m a = m * a

Rearranging the equation, acceleration is given in terms of [ SecondLawRewrite.hs]:

3.2.7.2. Second Law (Rewrite)

        module SecondLawRewrite where

a :: Float -> Float -> Float
a f m = (1 / m) * f

However, if m is assumed to be 1, a = (1 / 1) * f = f. So, rather than assign mass to a camera and try to apply forces, it's possible to simply apply acceleration as a (configurable) constant term directly. Linear integrators in the com.io7m.jcamera package are represented as 8-tuples (a, c, d, i, ms, sf, sr, su) where:

3.2.7.3. Linear integrator components

a is the acceleration to be applied, given in units-per-second-per-second.
c is the camera to be affected.
d is the drag factor.
i is an input.
ms is the maximum speed for the camera, in units-per-second.
sf current forward speed of the camera, in units-per-second.
sr current right speed of the camera, in units-per-second.
su current up speed of the camera, in units-per-second.

The meaning of units mentioned above is application specific. An application might choose to map units to meters, or miles, or any other arbitrary measure of distance.

As mentioned, an integrator makes changes to the position and orientation of a camera over a given delta time period. In most simulations, the camera will be updated at a fixed rate of something approaching 60 times per second. The delta time in this case would be given by delta = 1.0 / 60.0 = 0.0166666.... The integrator calculates a speed for each of the three (right, up, forward) axes in turn based on the current linear acceleration/deceleration values, and the data from the associated input, and tells the associated camera to move based on the resulting speeds.

For the forward axis, the integrator calculates a forward speed sfr based on the previous forward speed sf, the state of the input i, the acceleration a, and the drag factor d, and increases the camera position by sfr units along the forward axis. The forward speed is clamped to the configurable range [-ms, ms]. Specifically, the procedure is given by [ IntegratorForward.hs]:

3.2.7.4. Integrator (forward)

        module IntegratorForward where

import qualified Clamp
import qualified Vector3f
import qualified Input

forward_speed :: Input.T -> Float -> Float -> Float -> Float
forward_speed i sf a delta =
  if (Input.is_moving_forward i) 
  then sf + (a * delta) 
  else sf

backward_speed :: Input.T -> Float -> Float -> Float -> Float
backward_speed i sf a delta =
  if (Input.is_moving_backward i) 
  then sf - (a * delta) 
  else sf

forward :: (Vector3f.T, Vector3f.T, Float, Input.T, Float, Float, Float) -> Float -> (Vector3f.T, Float)
forward (p, v_forward, sf, i, a, d, ms) delta =
  let
    sf0 = backward_speed i (forward_speed i sf a delta) a delta
    sf1 = Clamp.clamp sf0 (-ms, ms)
    pr  = Vector3f.add3 p (Vector3f.scale v_forward (sf1 * delta))
    sfr = sf1 * (d ** delta)
  in
    (pr, sfr)

The drag factor is a configurable value that specifies how the camera will slow down over time. Ideally, when the user is not telling the camera to move, the camera is either stationary or on its way to becoming stationary. A drag factor d will result in a speed s' by s' = s * (d ** delta). Intuitively, the drag factor can be seen as the fraction of the original speed that will remain after one second of not receiving any acceleration. If d = 0.0, any object not having acceleration applied will immediately stop. If d = 1.0, an object will continue moving indefinitely [3]. A drag factor of 0.0 will also imply an overall movement speed penalty due to the way integration is performed. Usually, a drag factor of 0.0 is a bad idea - values closer to 0.0001 give the same abrupt behaviour but with slightly smoother results and less of a movement speed penalty.

Integration for the other axes is identical, modulo the parts of the input that are sampled [ IntegratorRight.hs] and [ IntegratorUp.hs]:

3.2.7.5. Integrator (right)

        module IntegratorRight where

import qualified Clamp
import qualified Vector3f
import qualified Input

right_speed :: Input.T -> Float -> Float -> Float -> Float
right_speed i sf a delta =
  if (Input.is_moving_right i) 
  then sf + (a * delta) 
  else sf

left_speed :: Input.T -> Float -> Float -> Float -> Float
left_speed i sf a delta =
  if (Input.is_moving_left i) 
  then sf - (a * delta) 
  else sf

right :: (Vector3f.T, Vector3f.T, Float, Input.T, Float, Float, Float) -> Float -> (Vector3f.T, Float)
right (p, v_right, sf, i, a, d, ms) delta =
  let
    sf0 = left_speed i (right_speed i sf a delta) a delta
    sf1 = Clamp.clamp sf0 (-ms, ms)
    pr  = Vector3f.add3 p (Vector3f.scale v_right (sf1 * delta))
    sfr = sf1 * (d ** delta)
  in
    (pr, sfr)

3.2.7.6. Integrator (up)

        module IntegratorUp where

import qualified Clamp
import qualified Vector3f
import qualified Input

up_speed :: Input.T -> Float -> Float -> Float -> Float
up_speed i sf a delta =
  if (Input.is_moving_up i) 
  then sf + (a * delta) 
  else sf

down_speed :: Input.T -> Float -> Float -> Float -> Float
down_speed i sf a delta =
  if (Input.is_moving_down i) 
  then sf - (a * delta) 
  else sf

up :: (Vector3f.T, Vector3f.T, Float, Input.T, Float, Float, Float) -> Float -> (Vector3f.T, Float)
up (p, v_up, sf, i, a, d, ms) delta =
  let
    sf0 = down_speed i (up_speed i sf a delta) a delta
    sf1 = Clamp.clamp sf0 (-ms, ms)
    pr  = Vector3f.add3 p (Vector3f.scale v_up (sf1 * delta))
    sfr = sf1 * (d ** delta)
  in
    (pr, sfr)

The type of linear integrators in the com.io7m.jcamera is JCameraFPSStyleLinearIntegratorType, with the default implementation being JCameraFPSStyleLinearIntegrator.

3.2.8

Angular Integrators

An angular integrator updates the orientation of a camera over time.

Integration of orientation occurs in almost exactly the same manner as integration of position; orientation is treated as a pair of scalar rotations around two axes, and the rotation values are increased by speed values calculated from acceleration values for each axis. Integration of rotations around the vertical axis is given by [ IntegratorAngularVertical.hs]:

3.2.8.1. Integrator (vertical)

        module IntegratorAngularVertical where

import qualified Clamp
import qualified Input

vertical :: (Float, Float, Input.T, Float, Float, Float) -> Float -> (Float, Float)
vertical (v, sv, i, a, d, ms) delta =
  let
    sf0 = sv + ((Input.rotation_vertical i) * a * delta)
    sf1 = Clamp.clamp sf0 (-ms, ms)
    vr  = v + (sf1 * delta)
    sfr = sf1 * (d ** delta)
  in
    (vr, sfr)

Note that the acceleration around the axis is multiplied by the rotation coefficients taken from the input.

Rotation around the horizontal axis is identical, except that the actual camera itself may clamp rotations around the horizontal axis. The reason for this is simple: If rotations are not clamped, and the user rotates the camera upwards or downwards, there comes a point where the camera's rotation value wraps around and the camera begins to rotate in the opposite direction, as illustrated:

3.2.8.2. Rotation wrapping

The practical result of the above wrapping is that the user would, for example, be rotating the camera up towards the ceiling, the camera would reach the limit of rotation, and suddenly the camera would be facing the opposite direction and rotating down towards the floor again. This behaviour would be irritating, so cameras may optionally clamp rotations and are required to indicate when clamping occurs so that the integrator can zero the speed of rotation around that axis. The reason for the zeroing of the rotation speed is that if the speed were not zeroed, and the rotation around the axis was proceeding at, say, 100 radians per second, the user would have to cause the rotation to decrease by over 100 radians per second in the opposite direction in order to get the camera to rotate at all. In effect, the camera would appear to reach the limit of rotation, stop, and then the user would have to scrub the mouse repeatedly in the opposite direction in order to get rotation to begin again in the opposite direction.

The type of angular integrators in the com.io7m.jcamera is JCameraFPSStyleAngularIntegratorType, with the default implementation being JCameraFPSStyleAngularIntegrator.

3.2.9

Aggregate Integrators

Usually, a user will want cameras to both move and rotate, as opposed to just one or the other. The com.io7m.jcamera package provides the JCameraFPSStyleIntegratorType which aggregates both the linear and angular integrators, with the default implementation given by JCameraFPSStyleIntegrator.

3.3

Spherical Camera

3.3.1. Overview
3.3.2. Camera Behaviour
3.3.3. Camera Mathematics
3.3.4. Camera Implementation
3.3.5. Input
3.3.6. Integrators
3.3.7. Linear Integrators
3.3.8. Angular Integrators
3.3.9. Aggregate Integrators

3.3.1

Overview

Most real-time strategy games implement some variation of a so-called spherical camera (also sometimes known as an orbital camera). A spherical camera always points towards, and stays a given distance from, a target point.

One of the classic examples of this type of camera was implemented in Bungie's Myth II: Soulblighter.

3.3.1.1. Myth II: Soulblighter

The camera described here implements a useful subset of the capabilities of Myth II's camera system [4] .

A restricted form of this camera is present in Blizzard's Starcraft II. The mouse-control scheme for Starcraft's camera is generally considered to be the definitive one amongst real-time strategy games, and the camera described here shamelessly duplicates it.

It is recommended that the reader fully understand the implementation and mathematics of fps-style cameras as most of the implementation described here uses the same approach and concepts.

3.3.2

Camera Behaviour

A spherical camera remains at a given radius from a movable target point. The orientation of the camera is derived from a heading angle and an incline angle.

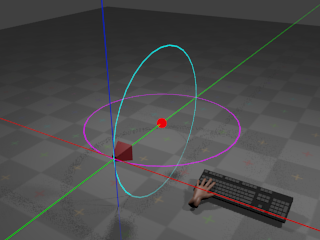
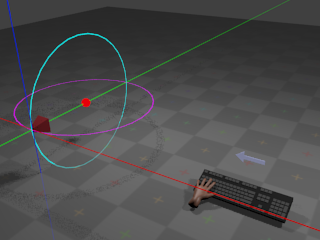
With no input from the mouse, the camera remains at its current orientation:

3.3.2.1. No input

The red sphere indicates the target point. The camera remains at a given radius from the target point, with the cyan ring indicating the path that the camera would take if the incline were to change, and the magenta ring indicating the path that the camera would take if the heading were to change. If the user presses the whatever key is assigned to orbit left, the camera heading angle begins to decrease at a configurable rate. This results in the camera rotating horizontally around the target point:

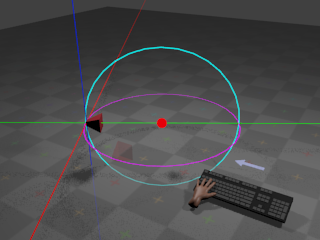
3.3.2.2. Orbit Heading

If the user presses whatever key is assigned to orbit right, the camera begins to rotate around the same arc but in the opposite direction.

If the user presses whatever key is assigned to orbit up, the camera incline angle begins to increase at a configurable rate. This results in the camera rotating vertically around the target point:

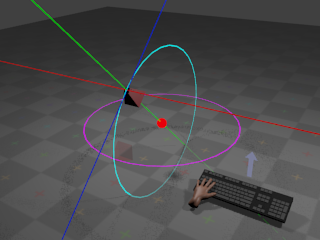
3.3.2.3. Orbit Incline

If the user presses whatever key is assigned to orbit down, the camera begins to rotate around the same arc but in the opposite direction.

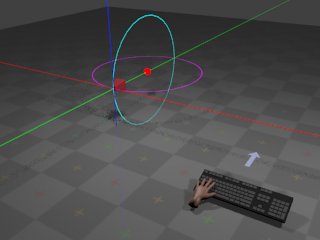
If the user presses whatever key is assigned to zoom out, the radius begins to increase at a configurable rate. This results in the camera giving the effect of zooming out:

3.3.2.4. Zoom

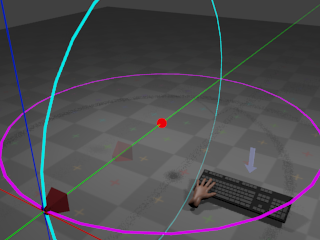
If the user presses whatever key is assigned to zoom in, the radius begins to decrease at a configurable rate. This results in the camera giving the effect of zooming in.

The target point can also move according to user input:

3.3.2.5. Target point movement

3.3.2.6. Target point movement

Whether target point movement occurs due to keyboard or mouse input is a matter of taste. The implementation described here provides both. Movement of the target point occurs along directions derived from the camera's current orientation. When the user instructs the target point to move up, the point begins to move towards positive infinity on the global Y axis. When the user instructs the target point to move forward, the target point begins to move along the direction defined by projecting the camera's current forward vector onto the horizontal plane. When the user instructs the target point to move right, the target point begins to move along the direction defined by projecting the camera's current right vector onto the horizontal plane. The precise definitions of these vectors are given in the following section on the mathematics of the camera.

3.3.2.7. Right and Forward

Moving the target point via keyboard input works in a familiar and unsurprising manner: When the user presses whatever key is assigned to a particular direction, the camera moves in that direction until the user releases the key.

Moving the target point via mouse input is more complicated, however. Mouse movement is provided by both dragging and edge scrolling. When the user drags the mouse in a given direction, the camera appears to move in the opposite direction by an amount proportional to the drag distance. When the user moves the mouse cursor to the edge of the screen, the camera appears to move in at a constant rate in a direction relative to the edge of the screen, until the user moves the mouse cursor away from that edge. These descriptions are somewhat vague, and a more formal description is given in the section on camera mathematics.

3.3.3

Camera Mathematics

A spherical camera can be represented as a 4-tuple (t, h, i, r), where t is the position of the target point, h is an angle around the global Y axis (the heading), i is an angle around the local X axis in radians (the incline), and r is the camera's distance from the target point (the radius). Astute readers will notice that the defined angles are coordinates in a spherical coordinate system, and therefore the movement of the camera around the target point always describes a sphere of radius r.

As with fps-style cameras, in order to implement forward/backward and left/right movement (and to derive a final view matrix so that the camera can be used to produce a viewing transform for 3D graphics), it's necessary to derive a 3-tuple of orthonormal direction vectors (forward, right, up) from the camera's angles and radius.

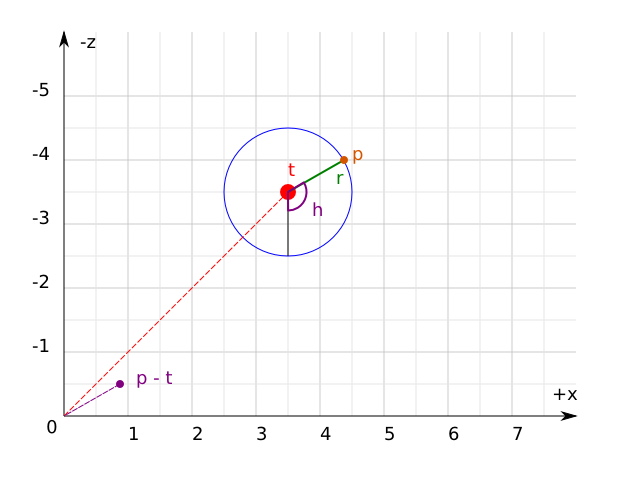
In order to derive the vectors, it's necessary to first work out the orientation of the camera. In order to calculate a full viewing transform, it's also necessary to calculate the actual world-space position p of the camera. As stated in the description of the camera behaviour, the camera is always oriented towards t. The mathematics of determining the camera's world-space position and orientation can be simplified if t is considered as the origin of a new local coordinate system that will be referred to as target-space. Transforming a world-space position w to target-space simply requires subtracting t from w. Transforming a target-space position u to world-space requires adding t to u. The following diagram illustrates all of the above, flattened onto the X/Z (horizontal) plane for ease of viewing:

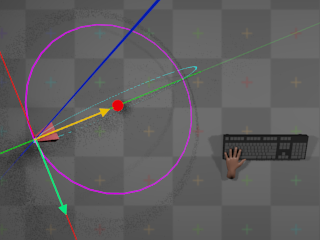
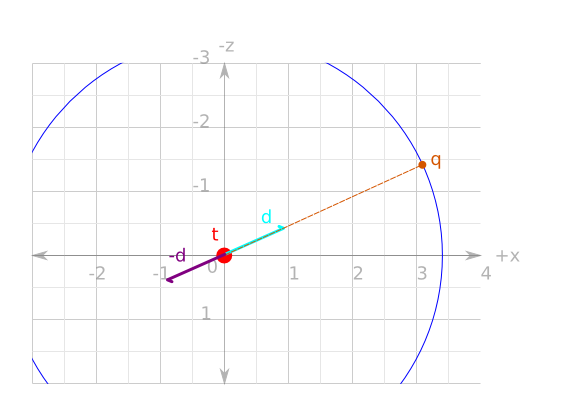
3.3.3.1. Camera configuration on X/Z

Firstly, then, to calculate the target-space camera position q the same equations are used as were used when calculating the direction vectors for the fps-style camera. Firstly, a direction vector d is calculated that points towards q from the origin:

3.3.3.2. x of d

3.3.3.3. y of d

3.3.3.4. z of d

Then, q is simply d scaled by r:

3.3.3.5. Target-space Q

q = Vector3f.scale d r

The world-space camera position p is simply q added to t:

3.3.3.6. World-space P

p = Vector3f.add3 q t

As stated, the aim is to construct a forward vector that points towards t from p. This is simply the negation of d:

3.3.3.7. Forward

forward = Vector3f.normalize (Vector3f.scale d -1)

3.3.3.8. Camera configuration on X/Z

Constructing the up vector for the camera is achieved by performing the exact same calculation as for the forward vector but with i - (π / 2). Intuitively, this works by calculating q as if it had been orbited downwards around the sphere, and then taking the negation of the resulting direction vector as normal:

3.3.3.9. Up

Finally, calculating the right vector is simply the cross product of the forward and up vectors.

3.3.3.10. Right

right = Vector3f.cross forward up

As stated earlier, forward/backward and left/right movement occurs only on the horizontal plane. Because the camera is not allowed to roll, the calculated right vector is always parallel to the horizontal plane and can therefore be used directly. Because the camera inclination is variable, however, the calculated forward vector is only parallel to the horizontal plane when i = 0. It's therefore necessary to calculate a forward_on_xz vector that is always parallel to the horizontal plane. This is achieved by projecting the forward vector onto the X/Z plane via a simple orthographic projection:

3.3.3.11. Forward on X/Z

project :: Vector3f.T -> Vector3f.T
project v =
  let vx = Vector3f.x v
      vz = Vector3f.z v
  in Vector3f.normalize (Vector3f.V3 vx 0.0 vz)

forward_on_xz :: Vector3f.T
forward_on_xz = project forward

There is an issue here: The projection of the forward vector resulting from an incline of exactly (π / 2) or (-π / 2) radians results in a forward vector equal to (0, ±1, 0), the projection of which is the zero vector (0, 0, 0). This means that when the camera is looking directly up towards (or directly down upon) the target position, the camera cannot be moved forwards or backwards. In practice, it is rare that the incline will be exactly either these values. The problem can be worked around entirely by clamping the possible incline ranges to [(π / 2) + e, (-π / 2) - e], where e is an arbitrary very small value.

A complete listing of all the equations given so far, using the default inclination and heading angles, and the default camera position is as follows [ ExampleSphericalDefaultVectors.hs]:

3.3.3.12. Default Vectors

        module ExampleSphericalDefaultVectors where

import qualified Vector3f

heading :: Float
heading = -pi / 2.0

incline :: Float
incline = 0

radius :: Float
radius = 8

target :: Vector3f.T
target = Vector3f.V3 0 1 4

direction :: Float -> Float -> Vector3f.T
direction heading incline =
  let
    x = (cos heading) * (cos incline)
    y = sin incline
    z = -((cos incline) * (sin heading))
  in
    Vector3f.V3 x y z

d :: Vector3f.T
d = direction heading incline

q :: Vector3f.T
q = Vector3f.scale d radius

p :: Vector3f.T
p = Vector3f.add3 q target

forward :: Vector3f.T
forward = Vector3f.normalize (Vector3f.scale d (-1.0))

up :: Vector3f.T
up =
  let d = direction heading (incline - (pi / 2.0)) in
    Vector3f.normalize (Vector3f.scale d (-1.0))

right :: Vector3f.T
right = Vector3f.cross forward up

project :: Vector3f.T -> Vector3f.T
project v =
  let vx = Vector3f.x v
      vz = Vector3f.z v
  in Vector3f.normalize (Vector3f.V3 vx 0.0 vz)

forward_on_xz :: Vector3f.T
forward_on_xz = project forward

Movement of the target point is achieved identically to the way fps-style cameras move, except that the forward_on_xz vector is used instead of the ordinary forward vector for forward/backward movement, and the global Y axis is used for up/down movement instead of the camera's up vector. View matrix calculating is also identical, using the calculated forward, right, and up vectors, and p for the translational components.

In order to implement mouse control over movement of the target point, it's necessary to somehow map two-dimensional mouse cursor movements to three-dimensional camera movements. All windowing systems tend to use system-specific conventions: Some windowing systems place (0, 0) at the top-left corner of the window, and others place (0, 0) at the bottom-left corner. In order to get system-independent and display-density-independent mouse control, the com.io7m.jcamera package borrows a concept from OpenGL: normalized device coordinates (albeit in a two-dimensional form). In normalized device space, the origin (0, 0) is in the center of the screen. The rightmost edge of the screen is x = 1, the leftmost edge of the screen is x = -1, the topmost edge is y = 1, and the bottommost ege is y = -1:

3.3.3.13. Normalized Device Space

The translation to normalized device coordinates from screen coordinates is simple, although slightly different equations are needed for systems that use a top-left origin as opposed to a bottom-left origin [ NormalizedDevice.hs]:

3.3.3.14. Screen To Normalized Device

        module NormalizedDevice where

import qualified Vector3f

width :: Float
width = 640.0

height :: Float
height = 480.0

to_ndc_from_top_left :: (Integer, Integer) -> (Float, Float)
to_ndc_from_top_left (sx, sy) =
  let
    center_x = width / 2.0
    center_y = height / 2.0
    rx = ((fromIntegral sx - center_x) / width) * 2.0
    ry = ((fromIntegral sy - center_y) / height) * 2.0
  in
    (rx, ry)

to_ndc_from_bottom_left :: (Integer, Integer) -> (Float, Float)
to_ndc_from_bottom_left (sx, sy) =
  let
    center_x = width / 2.0
    center_y = height / 2.0
    rx = ((fromIntegral sx - center_x) / width) * 2.0
    ry = ((fromIntegral sy - center_y) / height) * 2.0
  in
    (rx, -ry)

Given an arbitrary cursor position expressed as normalized device coordinates, it's then possible to determine if the cursor is at one or more of the screen edges. This is how edge scrolling is implemented. For example, if the cursor is at (1, 1), then it means the cursor is at the extreme top-right corner of the screen. The simple fact that a given cursor either is or isn't at a particular edge can be used as a discrete input. For the spherical camera described here, if the cursor is moved to the top edge of the screen, it is as if the user had pressed whatever key is assigned to forward. The camera continues moving in that direction until the cursor is moved away from the edge. If the cursor is moved to the right edge of the screen, it is as if the user had pressed whatever key is assigned to right. If the cursor is at one of the corners, it is as if the user had pressed whatever keys are assigned to the two relevant edges.

For the other form of mouse control - dragging - the same system is used to map screen-space mouse coordinates to normalized device coordinates. However, the coordinates of the mouse are only taken into account when the relevant mouse button is being held [5] . The offsets from the center of the screen are accumulated in the same manner as with the rotation coefficients for fps-style cameras, and are reset to (0, 0) periodically in the same manner. Additionally, the offsets are negated when the actual camera movement is applied. For example, if the user has dragged the mouse to the right, the camera is actually moved left. An intuitive way to think of this is to imagine that the objects that the camera is observing are on a sheet, and in order to look at a specific object that is laying to the right of the camera, the sheet must be pulled left to move the object into view. This is not actually mandated by the implementation in the com.io7m.jcamera package; the programmer is free to pass the non-negated offsets to the camera in order to move it [6]. An illustration of this (with the red frame indicating the camera's view):

3.3.3.15. Dragging

In practical terms, with the default settings, if the user drags the mouse downward, the camera moves as if the user had pressed whatever key is assigned to forward for the duration of the drag. If the user drags the mouse right, the camera moves as if the user had pressed left for the duration of the drag. The camera will correctly move diagonally if the user drags downward and right.

3.3.4

Camera Implementation

In the com.io7m.jcamera package, the interface exposed by a spherical camera is described by the JCameraSphericalType type. The actual implementation of the camera mathematics is given in the JCameraSpherical type.

Additionally, the incline angle i can be clamped to a given range (and is clamped by default).

3.3.5

Input

In the com.io7m.jcamera package, an input is a simple abstraction intended to keep integrators insulated from the platform-specific details of keyboard and mouse input.

As described in the section on fps-style camera input, input can categorized as discrete or continuous. The details of input for spherical cameras are slightly more complicated than for fps-style cameras due to the more complex control scheme.

An input for a spherical camera in the com.io7m.jcamera package is represented by the following data structure [ InputSpherical.hs]:

3.3.5.1. Input (Spherical)

        module InputSpherical (T (..)) where

data T = T {

  is_moving_backward_key    :: Bool,
  is_moving_backward_cursor :: Bool,

  is_moving_forward_key    :: Bool,
  is_moving_forward_cursor :: Bool,

  is_moving_left_key     :: Bool,
  is_moving_left_cursor  :: Bool,

  is_moving_right_key    :: Bool,
  is_moving_right_cursor :: Bool,

  is_moving_up        :: Bool,
  is_moving_down      :: Bool,

  moving_forward_continuous :: Float,
  moving_right_continuous   :: Float,

  is_orbiting_heading_positive :: Bool,
  is_orbiting_heading_negative :: Bool,
  is_orbiting_incline_positive :: Bool,
  is_orbiting_incline_negative :: Bool,

  is_zooming_in  :: Bool,
  is_zooming_out :: Bool
  
} deriving (Eq, Show)

In a similar manner to the fps-style camera input, pressing a key on the keyboard sets the corresponding boolean field in the input to true, setting it to false when the key is released. In order to account for the fact that some movements can be prompted by both the keyboard and mouse, there are separate fields for keyboard and cursor control. For example, moving a mouse to the right edge of the screen sets the is_moving_right_cursor field to true. The moving_forward_continuous and moving_right_continuous fields represent the accumulated dragging for the current time period.

In the com.io7m.jcamera package, spherical camera inputs are represented by the JCameraSphericalInput type, and mouse regions are represented by the JCameraSphericalMouseRegion type.

3.3.6

Integrators

Integrators are responsible for updating properties of cameras over time. They are divided into linear and angular types.

3.3.7

Linear Integrators

A linear integrator updates the position of a camera over time.

Linear integration of the camera is achieved in an almost identical manner to linear integration of fps-style cameras, with the addition of the changes of position caused by the continuous input from mouse dragging. Changes in radius (zooming) are also handled by the linear integrator.

Calculation of the forward velocity is given by the following equations [ IntegratorSphericalForward.hs]:

3.3.7.1. Integrator (forward)

        module IntegratorSphericalForward where

import qualified Clamp
import qualified Vector3f
import qualified InputSpherical

forward_speed :: InputSpherical.T -> Float -> Float -> Float -> Float
forward_speed i sf a delta =
  if (InputSpherical.is_moving_forward_key i || InputSpherical.is_moving_forward_cursor i)
  then sf + (a * delta)
  else sf

backward_speed :: InputSpherical.T -> Float -> Float -> Float -> Float
backward_speed i sf a delta =
  if (InputSpherical.is_moving_backward_key i || InputSpherical.is_moving_backward_cursor i)
  then sf - (a * delta)
  else sf

drag_forward_speed :: InputSpherical.T -> Float -> Float -> Float
drag_forward_speed i a delta =
  (InputSpherical.moving_forward_continuous i) * a * delta

forward :: (Vector3f.T, Vector3f.T, Float, InputSpherical.T, Float, Float, Float) -> Float -> (Vector3f.T, Float)
forward (p, v_forward_on_xz, sf, i, a, d, ms) delta =
  let
    sf0 = backward_speed i (forward_speed i sf a delta) a delta
    sf1 = Clamp.clamp sf0 (-ms, ms)
    sd  = drag_forward_speed i a delta
    sf2 = sf1 + sd
    pr  = Vector3f.add3 p (Vector3f.scale v_forward_on_xz (sf2 * delta))
    sfr = sf1 * (d ** delta)
  in
    (pr, sfr)

The first thing to note is the drag_forward_speed function: This calculates how much the camera should be moving in the forward direction based on the current accumulated continuous input. The forward speed calculated by the function is added to the current total speed after the total has been clamped to the speed limits. The reason for this is simply that the speed limits are usually set reasonably low in order to avoid the camera getting up to too high a speed when controlled by the keyboard, but the low speed limits also tend to mean that the user cannot drag the mouse fast enough to get a comfortable movement rate. Exceeding the speed limit temporarily is mildly distasteful, but relies on the fact that the user is physically limited by their own ability to fling a piece of plastic across a desktop, and so the speed of the camera should not become excessively high. An alternate solution would be to have two sets of speed limits, one for keyboard control and another for dragging. This is trivial to implement, but is not implemented here for the sake of keeping the implementation as easy to understand as possible.

There is also a limitation in the described integrator: The camera feels increasingly sluggish as the camera zooms out. This is purely a perceptual issue: If the camera is a very long way away from an object, then the camera has to move much further for there to be a perceived movement onscreen than it would have to move if it were very close to the object. Essentially, it's desirable for the camera to move faster the further away it is from the target point. The way this is achieved in the com.io7m.jcamera package is to associate a pair of functions scale_linear and scale_dragging with the integrator that are responsible for producing scaling factors when given the current radius (zoom). The linear speed, acceleration, and maximum speeds are scaled by scale_linear, and the extra speed produced by dragging is scaled by scale_dragging [ IntegratorSphericalForwardZoomScaled.hs]:

3.3.7.2. Integrator (forward, zoom-scaled)

        module IntegratorSphericalForwardZoomScaled where

import qualified Clamp
import qualified Vector3f
import qualified InputSpherical

type ScaleFunction = Float -> Float

forward_speed :: InputSpherical.T -> Float -> Float -> Float -> Float -> ScaleFunction -> Float
forward_speed i sf a zoom scale delta =
  let accel = (scale zoom) * (a * delta) in
    if (InputSpherical.is_moving_forward_key i || InputSpherical.is_moving_forward_cursor i)
    then sf + accel
    else sf

backward_speed :: InputSpherical.T -> Float -> Float -> Float -> Float -> ScaleFunction -> Float
backward_speed i sf a zoom scale delta =
  let accel = (scale zoom) * (a * delta) in
    if (InputSpherical.is_moving_backward_key i || InputSpherical.is_moving_backward_cursor i)
    then sf - accel
    else sf

drag_forward_speed :: InputSpherical.T -> Float -> Float -> ScaleFunction -> Float
drag_forward_speed i a zoom scale delta =
  (InputSpherical.moving_forward_continuous i) * a * (scale zoom) * delta

forward :: (Vector3f.T, Vector3f.T, Float, InputSpherical.T, Float, Float, Float, Float, (ScaleFunction, ScaleFunction)) -> Float -> (Vector3f.T, Float)
forward (p, v_forward_on_xz, sf, i, a, d, ms, zoom, (scale_linear, scale_dragging)) delta =
  let
    sf0 = backward_speed i (forward_speed i sf a delta) a delta
    sms = (scale_linear zoom) * ms
    sf1 = Clamp.clamp sf0 (-sms, sms)
    
    sd  = drag_forward_speed i a zoom scale_dragging delta
    sf2 = sf1 + sd

    pr  = Vector3f.add3 p (Vector3f.scale v_forward_on_xz (sf2 * delta))
    sfr = sf1 * (d ** delta)
  in
    (pr, sfr)

Experimentation has shown that using the same function for scale_dragging and scale_linear tends to give results that are good for one and not the other. The default choice for scale_dragging is simply the identity function, and the default choice for scale_linear is the square root function. This effectively scales dragging directly by the current zoom level, and scales linear movement (caused by edge scrolling and the keyboard) by the square root of the current zoom level. The same scaling is applied equally to forward and rightward movement.

3.3.8

Angular Integrators

An angular integrator updates the orientation of a camera over time.

Rotation by the incline angle is identical, except that the actual camera itself may optionally clamp the incline angle to work around the documented projection issue.

The type of angular integrators in the com.io7m.jcamera is JCameraSphericalAngularIntegratorType, with the default implementation being JCameraSphericalAngularIntegrator.

3.3.9

Aggregate Integrators

Usually, a user will want cameras to both move and rotate, as opposed to just one or the other. The com.io7m.jcamera package provides the JCameraSphericalIntegratorType which aggregates both the linear and angular integrators, with the default implementation given by JCameraSphericalIntegrator.

API Reference

4.1. Javadoc

4.1

Javadoc

API documentation for the package is provided via the included Javadoc.

[0]

http://semver.org

[1]

Most camera systems documented (usually in blogs) online either describe only the mathematics and fail to describe the intricacies of driving the system with input, or violently mash all of the mathematics into an existing assumption-ridden input and rendering system - meaning that the reader has to fully understand an input system or rendering system that they may not ever have even seen before just to understand how the camera works.

[2]

While it may be more intuitive to think of the rightmost position being 1.0 and the leftmost position being -1.0, recall that a positive rotation represents a counter-clockwise rotation around an axis when looking towards negative infinity on that axis. For a first-person camera system, a negative rotation on the vertical axis therefore represents a turn to the right.

[3]

This is obviously the correct physical behaviour for an object that is not being influenced by any forces, but it's not very useful behaviour for a camera system!

[4]

Myth II allowed the target point to orbit around the camera, as opposed to only allowing the camera to orbit around the target point. This capability is not widely useful and complicates the implementation of the camera significantly, and so is omitted here.

[5]

Starcraft II uses the middle mouse button for dragging. The com.io7m.jcamera package leaves it to the programmer to decide.

[6]

The "inverted" behaviour is the default camera behaviour in Starcraft II, and is therefore used here as the default.